patulong naman about sa maxima and minima
point A and B are opposite to each other on the shores of a straight river 5km wide. point F is on the same shore as B but K kilometers down the river from B. Atelephone company wishes to lay a cable from A to f where the cost per km of the cable on land is 10,000 US dollar and under the water is 12,500 US dollar. Let P be a point on the same shoreas B annd Fso that the cable runs from A to P to F.(a)if X kilometer is the distance from B to P obtain an equation defining (x) if C(x) dollars is the total cost of laying cable and state the domain of C.
(b) if K-2 solve the value of X for wich the cost (C) of laying cable is least as will as the least cost.
- Log in to post comments


To answer a.), we need a
To answer a.), we need a figure. For me, it looks like this:
Adding additional details:
[!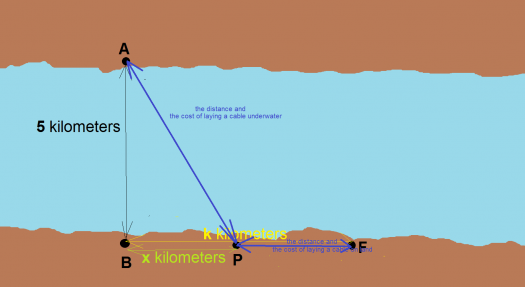
The total cost of laying the cable can be get by looking at a hint: The blue lines that connect the points A, P and F.
The total cost of laying the cable would be: cost of laying the cable underwater plus the cost of laying the cable on land. The equation needed according to the preceding figure above would be:
$$C(x) \space dollars = \left(\frac{12 500 \space dollars}{km}\right)\left(\sqrt{5^2 + x^2}\right) \space km + \left(\frac{10 000 \space dollars}{km}\right)(k - x) \space km$$
K is any value. The domain of the equation above is $[-\infty \bigcup \infty]$ but because there is no such thing as negative amount of dollars, the domain of the equation that makes sense is $\color{green}{[0 \bigcup \infty]}$ because we can practically put any value of $x$ in the equation without any worries of dividing by zero. The equation above is a continuous function.
b.) To get the value of $x$ which is the distance from point B to P that makes the total cost of laying the cable at minimum, we need to get the derivative of the equation below, given that $k = 2 \space kilometers$.
$$C \space dollars = \left(\frac{12 500 \space dollars}{km}\right)\left(\sqrt{5^2 + x^2}\right) \space km + \left(\frac{10 000 \space dollars}{km}\right)(2 - x) \space km$$
Now getting the derivative of the equation by implicit differentiation:
$$C \space dollars = \left(\frac{12 500 \space dollars}{km}\right)\left(\sqrt{5^2 + x^2}\right) \space km + \left(\frac{10 000 \space dollars}{km}\right)(2 - x) \space km$$ $$C = 12 500 \left(\sqrt{5^2 + x^2}\right) + 10 000(2 - x)$$ $$C = 12 500 \left(\sqrt{5^2 + x^2}\right) + 20 000 - 10000x$$ $$-20000 + C = 12 500 \left(\sqrt{5^2 + x^2}\right) - 10000x$$
Since constant + any number is a constant, so...
$$C = 12 500 \left(\sqrt{5^2 + x^2}\right) - 10000x$$
We can now do the implicit differentiation:
$$C = 12 500 \left(\sqrt{5^2 + x^2}\right) - 10000x$$ $$C = 12 500 \left(5^2 + x^2\right)^{\frac{1}{2}} - 10000x$$ $$\frac{d}{dx}(C) = 12 500 \frac{d}{dx}\left(\sqrt{5^2 + x^2}\right) - 10000\frac{d}{dx}(x)$$ $$0 = 12 500 \left( \left(\frac{1}{2}\right)(25 + x^2)^{\frac{1}{2} - 1} \frac{d}{dx}(25 + x^2)\right) - 10000 \frac{d}{dx}(x) $$ $$0 = 12 500 \left( \left(\frac{1}{2}\right)(25 + x^2)^{-\frac{1}{2}} (2x )\right) - 10000$$ $$0 = 12 500 \frac{x}{\sqrt{25 + x^2}} - 10000$$
We were able to get the derivative of the equation $C = 12 500 \left(\sqrt{5^2 + x^2}\right) + 10 000(2 - x)$. Now getting the value of $x$ of the derivative:
$$10000 = 12 500 \frac{x}{\sqrt{25 + x^2}}$$ $$\frac{4}{5} = \frac{x}{\sqrt{25 + x^2}}$$
The value of $x$ now is $6.6$.
So the distance from point B to P is $\color{green}{x = 6.6 \space kilometers}$.
sana makatulong...:-)