Below is the probability table of up to seven steps:
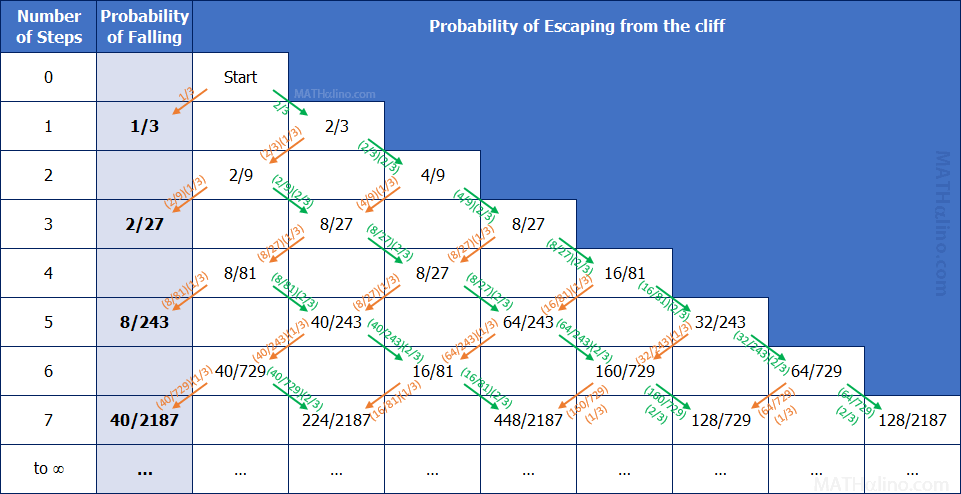
Click the picture to magnify
The orange arrow indicates one step towards the cliff and the green arrow indicates one step away from the cliff. The value inside the cell is the probability after taking n steps and the number in the arrow is the probability of taking that step. If two arrows are pointing on a cell, the value on that cell is the sum of the numbers in the arrows pointing to that cell.
One step to the left to fall off the cliff
Let
L = moving to the left (towards the cliff)
R = moving to the right (away from the cliff)
q = probability of taking a step toward the cliff = 1/3
p = probability of taking a step away from the cliff = 2/3
Q(n) = probability of falling in exactly n steps
Qn = probability of falling in at most n steps
Q = probability of falling off the cliff
Probability of falling in exactly 1 step
Number of ways = 1:
1. L
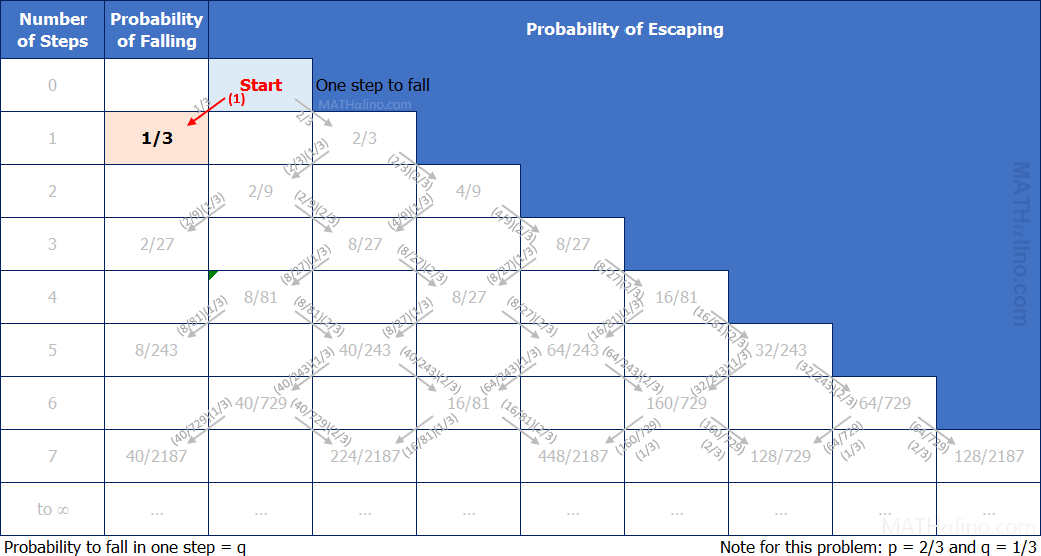
$Q(1) = 1 \times p^0q^1 = 1(2/3)^0 (1/3)^1 = 1/3$
The drunk man won't fall in two steps
Number of ways = 2
1. RL (red steps)
2. RR (green steps)
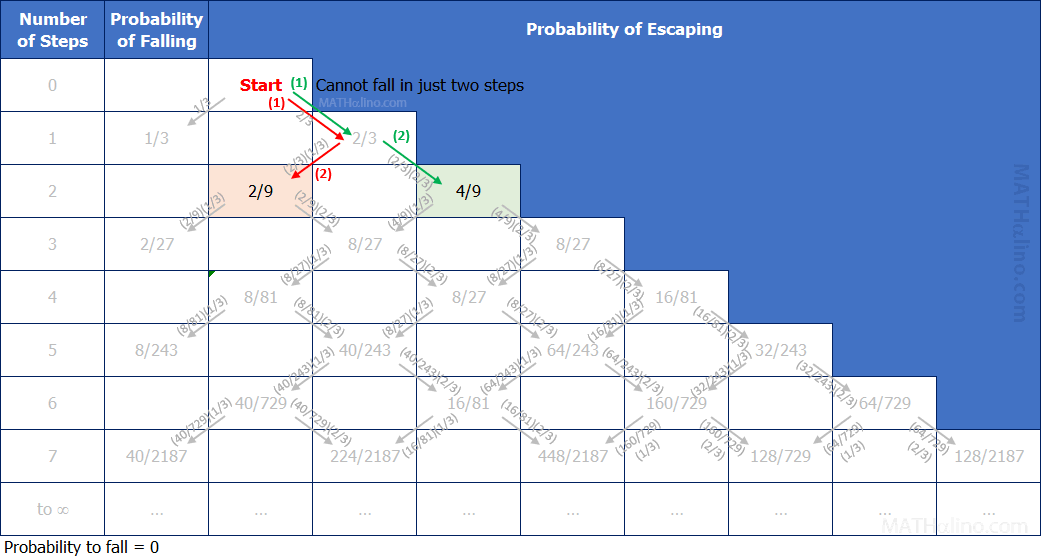
$Q(2) = 0$ ← Also true for all even-number of steps.
Probability of falling in exactly 3 steps
Number of ways
1. RLL
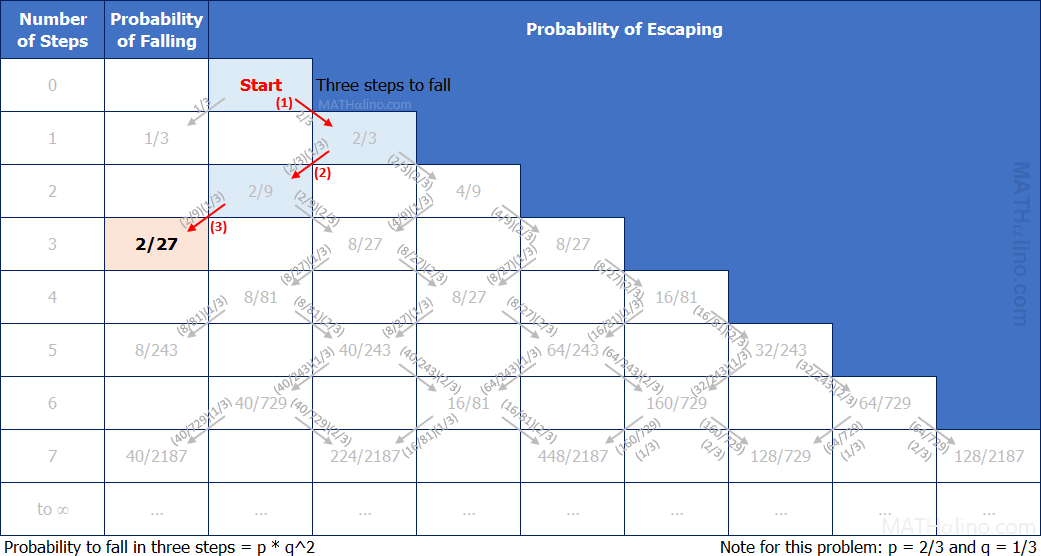
$Q(3) = 1 \times p^1q^2 = (2/3)^1 (1/3)^2 = 2/27$
Probability of falling in exactly 5 steps
Number of ways
1. RLRLL (red steps)
2. RRLLL (green steps)
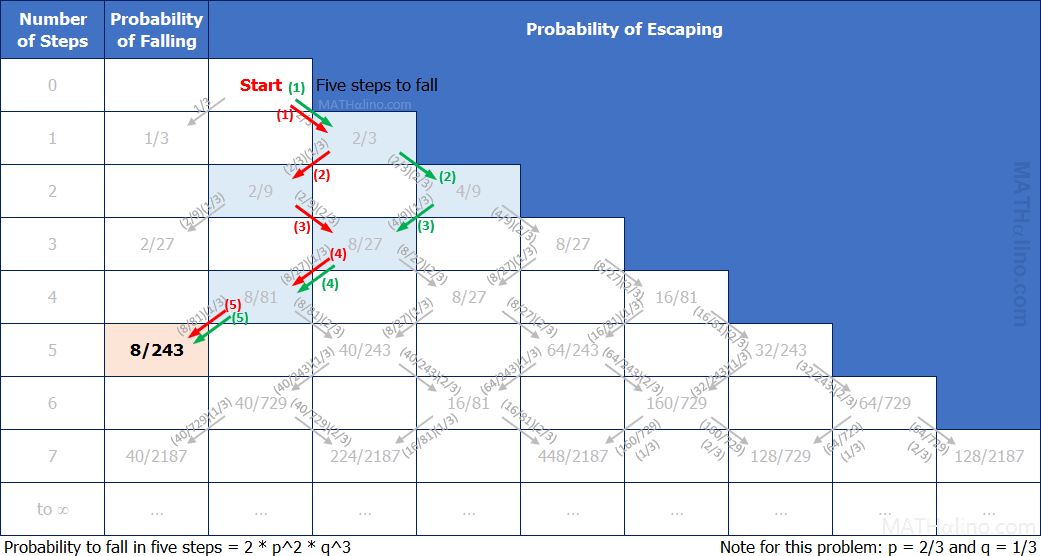
$Q(5) = 2 \times p^2q^3 = 2(2/3)^2 (1/3)^3 = 8/243$
Probability of falling in exactly 7 steps
Number of ways = 5
1. RLRLRLL (red steps)
2. RLRRLLL (pink steps)
3. RRLRLLL (blue steps)
4. RRLLRLL (green steps)
5. RRRLLLL (orange steps)
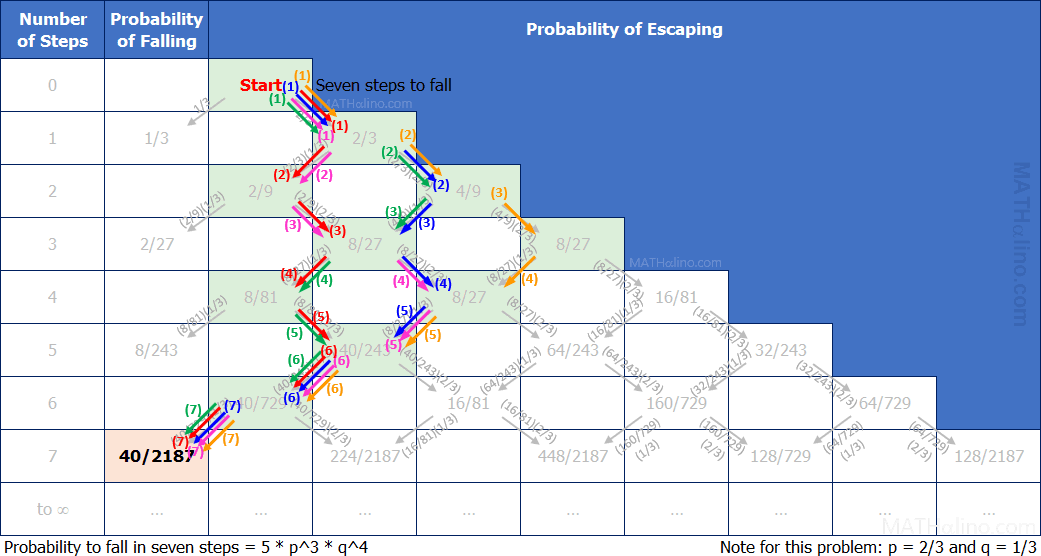
$Q(7) = 5 \times p^3q^4 = 5(2/3)^3(1/3)^4 = 40/2187$
In general, the probability of falling off the cliff in exactly n steps is
$Q(n) = \left[ \dfrac{(n - 1)!}{\left( \dfrac{n - 1}{2} + 1 \right)! \, \left( \dfrac{n - 1}{2} \right)!} \right] \, p^{(n - 1)/2} \, q^{(n - 1)/2 + 1}$
Note that n can only take odd numbers.
The probability of falling in at most n-steps is
$Q_n = Q(1) + Q(3) + Q(5) + ... + Q(n)$
$\displaystyle Q_n = \sum_{n = 1}^n \left[ \dfrac{(n - 1)!}{\left( \dfrac{n - 1}{2} + 1 \right)! \, \left( \dfrac{n - 1}{2} \right)!} \right] \, p^{(n - 1)/2} \, q^{(n - 1)/2 + 1}$
The probability of falling off the cliff for infinite number of steps is
$Q_n = Q(1) + Q(3) + Q(5) + ... + Q(n) + Q(n + 2) + ... $
$\displaystyle Q = \sum_{n = 1}^\infty \left[ \dfrac{(n - 1)!}{\left( \dfrac{n - 1}{2} + 1 \right)! \, \left( \dfrac{n - 1}{2} \right)!} \right] \, p^{(n - 1)/2} \, q^{(n - 1)/2 + 1}$
Where n = 1, 3, 5, 7, 9, 11, ...
On CASIO f(x)-991ES PLUS
For us to enter the equation into summation function of our calculator, let us revise our equation to x so that when we input x = 1, 2, 3, 4, ... the value of n = 1, 3, 5, 7, .... In this case, let
$n = 2x - 1$
The probability of falling off the cliff in exactly n steps
$Q(n) = \left[ \dfrac{(2x - 2)!}{x! \,(x - 1)!} \right] \, p^{(x - 1)} \, q^x$
The probability of falling in at most n-steps is
$\displaystyle Q_n = \sum_{x = 1}^x \left[ \dfrac{(2x - 2)!}{x! \, (x - 1)!} \right] \, p^{(x - 1)} \, q^x$
The probability of falling off the cliff for infinite number of steps is
$\displaystyle Q = \sum_{x = 1}^\infty \left[ \dfrac{(2x - 2)!}{x! \, (x - 1)!} \right] \, p^{(x - 1)} \, q^x$
Where $x = \frac{1}{2}(n + 1)$
Simple equation for the probability of falling off the cliff in infinite number of steps (Probability with Recursion)
The above equations are clearly complicated but it is a good start to understand the problem. A more general approach will greatly simplify the solution.
If the man steps to the left, the probability of falling Q = q. If he steps to the right with a probability of p, the probability of coming back to the starting point is pq. But q = Q, hence the probability of coming back to the starting point is pQ. The probability of making one more step to the left is therefore (pQ)Q. Thus, the total probability of falling is...
$Q = q + pQ^2$
$pQ^2 - Q + q = 0$
$Q = \dfrac{1 \pm \sqrt{1 - 4pq}}{2p}$
$Q = \dfrac{1 \pm \sqrt{1 - 4(1 - q)q}}{2(1 - q)}$
$Q = \dfrac{1 \pm \sqrt{1 - 4q + 4q^2}}{2(1 - q)}$
$Q = \dfrac{1 \pm \sqrt{(1 - 2q)^2}}{2(1 - q)}$
$Q = \dfrac{1 \pm (1 - 2q)}{2(1 - q)}$
Use
$P = \dfrac{1 - (1 - 2q)}{2(1 - q)}$
$Q = \dfrac{2q}{2(1 - q)}$
$Q = \dfrac{q}{1 - q}$
Hence,
$Q = \dfrac{q}{p}$
It is interesting to note that if the drunk man is exactly n steps away from the cliff, the probability of falling off the cliff is
$Q = \left( \dfrac{q}{p} \right)^n$
and the probability of escaping the cliff is
$P = 1 - \left( \dfrac{q}{p} \right)^n$
