March 2017

Problem
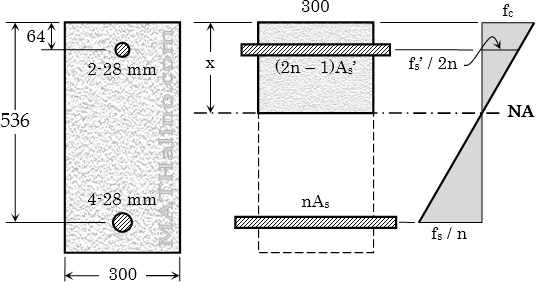
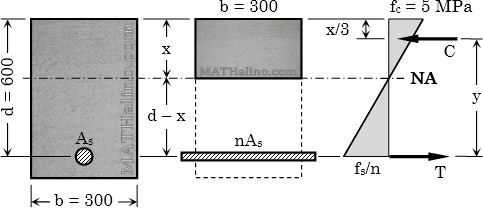
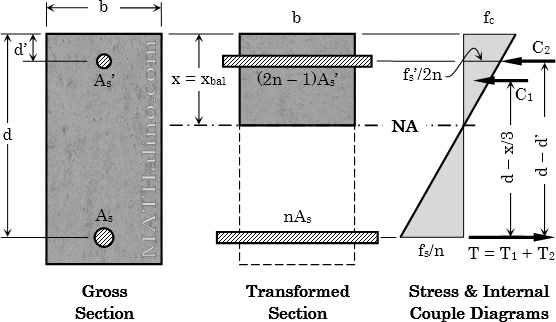
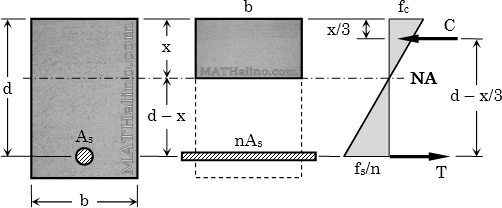
A 300 mm × 600 mm reinforced concrete beam section is reinforced with 4 - 28-mm-diameter tension steel at d = 536 mm and 2 - 28-mm-diameter compression steel at d' = 64 mm. The section is subjected to a bending moment of 150 kN·m. Use n = 9.

1. Find the maximum stress in concrete.
2. Determine the stress in the compression steel.
3. Calculate the stress in the tension steel.
 

Problem
The following are the dimensions of a concrete T-beam section

The beam is reinforced with 3-32 mm diameter bars in tension and is carrying a moment of 100 kN·m. Find the total compressive force in the concrete. Use n = 9.
 

Problem
A reinforced concrete beam 300 mm wide has an effective depth of 600 mm. It is reinforced with 4-32 mm diameter bars for tension. f’_c = 21 MPa and f_y = 275 MPa. Find the moment capacity of the beam.
 

Problem
A rectangular reinforced concrete beam with width of 250 mm and effective depth of 500 mm is subjected to 150 kN·m bending moment. The beam is reinforced with 4 – 25 mm ø bars. Use alternate design method and modular ratio n = 9.

1. What is the maximum stress of concrete?
2. What is the maximum stress of steel?
3. What is the total compressive force in concrete?

Problem
A rectangular concrete beam is reinforced in tension only. The width is 300 mm and the effective depth is 600 mm. The beam carries a moment of 80 kN·m which causes a stress of 5 MPa in the extreme compression fiber of concrete. Use n = 9.
1.   What is the distance of the neutral axis from the top of the beam?
2.   Calculate the required area for steel reinforcement.
3.   Find the stress developed in the steel.
 

Steps is for finding the required steel reinforcements of beam with known M_max and other beam properties using Working Stress Design method.

Given the following, direct or indirect:

Consider a relatively long simply supported beam shown below. Assume the load w_o to be increasing progressively until the beam fails. The beam will go into the following three stages:

1. Uncrack Concrete Stage – at this stage, the gross section of the concrete will resist the bending which means that the beam will behave like a solid beam made entirely of concrete.
2. Crack Concrete Stage – Elastic Stress range
3. Ultimate Stress Stage – Beam Failure