January 2011
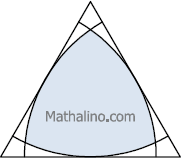
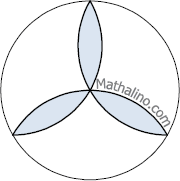
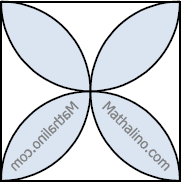
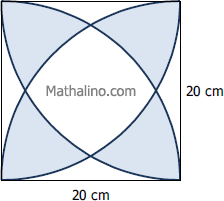
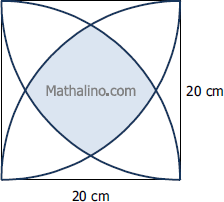
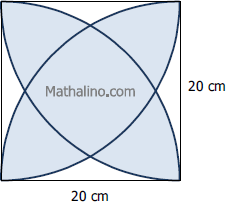
Arcs of quarter circles
- Read more about Arcs of quarter circles
- Log in or register to post comments
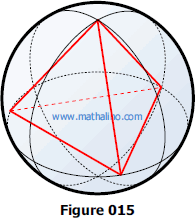
016 Radius of the sphere circumscribing a regular triangular pyramid
Example 016
Find the area of the surface and the volume of the sphere circumscribed about a regular tetrahedron of edge 25 cm. See Figure 015.
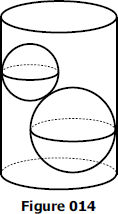
015 Two unequal balls inside the cylinder
Example 015
Two balls, one 15 cm in diameter and the other 10 cm in diameter, are placed in a cylindrical jar 20 cm in diameter, as shown in Figure 014. Find the volume of water necessary to cover them.
- Read more about 015 Two unequal balls inside the cylinder
- Log in or register to post comments
014 Water poured into a jar of marbles
Example 014
A boy who had discovered that 20 mm marbles fitted snugly into the bottom of a cylindrical jar, dropped in a fourth on top of the three and poured water enough into the jar to just cover them. How much water did he use?
- Read more about 014 Water poured into a jar of marbles
- Log in or register to post comments