Flanged bolt couplings
In shaft connection called flanged bolt couplings (see figure), the torque is transmitted by the shearing force P created in he bolts that is assumed to be uniformly distributed. For any number of bolts n, the torque capacity of the coupling is
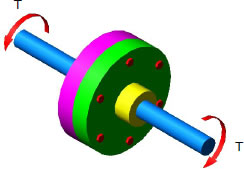
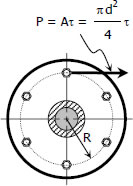
- Read more about Flanged bolt couplings
- Log in to post comments
Solution to Problem 325 Torsion
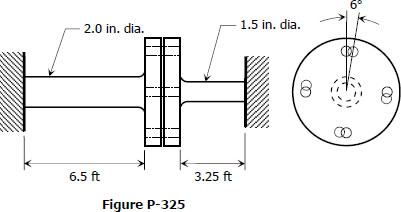
Problem 325
The two steel shaft shown in Fig. P-325, each with one end built into a rigid support have flanges rigidly attached to their free ends. The shafts are to be bolted together at their flanges. However, initially there is a 6° mismatch in the location of the bolt holes as shown in the figure. Determine the maximum shearing stress in each shaft after the shafts are bolted together. Use G = 12 × 106 psi and neglect deformations of the bolts and flanges.
- Read more about Solution to Problem 325 Torsion
- Log in to post comments
Solution to Problem 324 Torsion
Problem 324
The compound shaft shown in Fig. P-324 is attached to rigid supports. For the bronze segment AB, the maximum shearing stress is limited to 8000 psi and for the steel segment BC, it is limited to 12 ksi. Determine the diameters of each segment so that each material will be simultaneously stressed to its permissible limit when a torque T = 12 kip·ft is applied. For bronze, G = 6 × 106 psi and for steel, G = 12 × 106 psi.
- Read more about Solution to Problem 324 Torsion
- Log in to post comments
Solution to Problem 323 Torsion
Problem 323
A shaft composed of segments AC, CD, and DB is fastened to rigid supports and loaded as shown in Fig. P-323. For bronze, G = 35 GPa; aluminum, G = 28 GPa, and for steel, G = 83 GPa. Determine the maximum shearing stress developed in each segment.
- Read more about Solution to Problem 323 Torsion
- Log in to post comments
Solution to Problem 322 Torsion
Problem 322
A solid steel shaft is loaded as shown in Fig. P-322. Using G = 83 GPa, determine the required diameter of the shaft if the shearing stress is limited to 60 MPa and the angle of rotation at the free end is not to exceed 4 deg.
- Read more about Solution to Problem 322 Torsion
- Log in to post comments
Solution to Problem 320 Torsion
Problem 320
In Prob. 319, determine the ratio of lengths b/a so that each material will be stressed to its permissible limit. What torque T is required?
- Read more about Solution to Problem 320 Torsion
- 2 comments
- Log in to post comments
Solution to Problem 319 Torsion
Problem 319
The compound shaft shown in Fig. P-319 is attached to rigid supports. For the bronze segment AB, the diameter is 75 mm, τ ≤ 60 MPa, and G = 35 GPa. For the steel segment BC, the diameter is 50 mm, τ ≤ 80 MPa, and G = 83 GPa. If a = 2 m and b = 1.5 m, compute the maximum torque T that can be applied.
- Read more about Solution to Problem 319 Torsion
- Log in to post comments
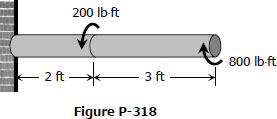
Solution to Problem 318 Torsion
Problem 318
A solid aluminum shaft 2 in. in diameter is subjected to two torques as shown in Fig. P-318. Determine the maximum shearing stress in each segment and the angle of rotation of the free end. Use G = 4 × 106 psi.
- Read more about Solution to Problem 318 Torsion
- 1 comment
- Log in to post comments
316 Permissible Torque That Can Be Applied to a Compound Shaft
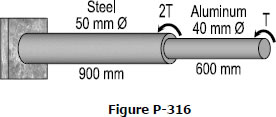
Problem 316
A compound shaft consisting of a steel segment and an aluminum segment is acted upon by two torques as shown in Fig. P-316. Determine the maximum permissible value of T subject to the following conditions: τst ≤ 83 MPa, τal ≤ 55 MPa, and the angle of rotation of the free end is limited to 6°. For steel, G = 83 GPa and for aluminum, G = 28 GPa.
315 Power Applied and Removed at Shaft Gears
Problem 315
A 5-m steel shaft rotating at 2 Hz has 70 kW applied at a gear that is 2 m from the left end where 20 kW are removed. At the right end, 30 kW are removed and another 20 kW leaves the shaft at 1.5 m from the right end. (a) Find the uniform shaft diameter so that the shearing stress will not exceed 60 MPa. (b) If a uniform shaft diameter of 100 mm is specified, determine the angle by which one end of the shaft lags behind the other end. Use G = 83 GPa.
- Read more about 315 Power Applied and Removed at Shaft Gears
- Log in to post comments