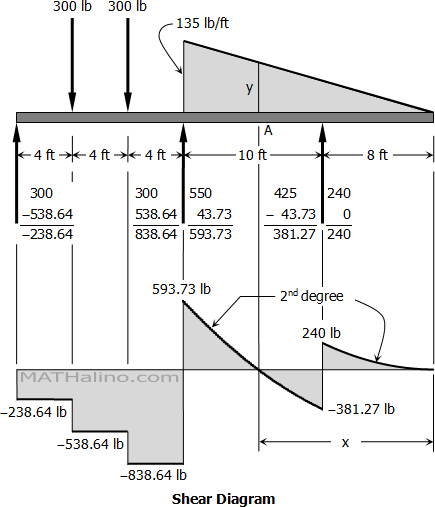
reaction at the support
Problem 007-cb | Analysis of Cabled Frame
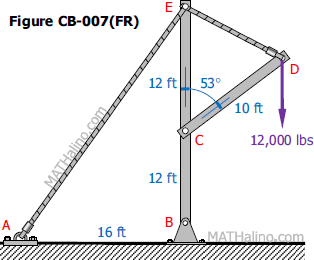
Problem 007-cb
In the structure shown in Fig. CB-007(FR), members BCE, and CD are assumed to be solid rigid members. Members AE and DE are cables. For this structure, determine the
reaction at B.
- Read more about Problem 007-cb | Analysis of Cabled Frame
- Log in or register to post comments
Problem 006-fr | Analysis of Simple Frame
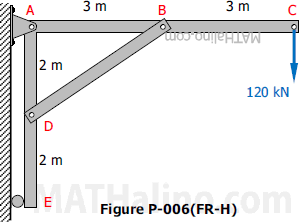
Problem 006-fr
In the structure shown in Fig. P-006(FR-H), all members are assumed to be solid rigid members. The system is pinned to the wall at point A and supported by a roller at point E. Calculate the force on member BD and the reactions at A and E.
- Read more about Problem 006-fr | Analysis of Simple Frame
- Log in or register to post comments
Problem 005-mm | Method of Members
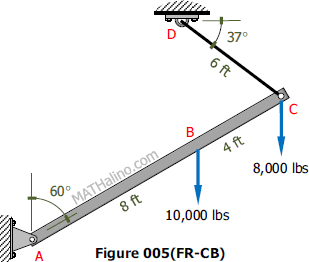
Problem 005-cb
For the cabled structure in Fig. 005(FR-CB), member ABC which is assumed to be rigid is pinned at A and held in equilibrium by cable CD. For this structure, determine the reaction at A and the tension in the cable.
- Read more about Problem 005-mm | Method of Members
- Log in or register to post comments
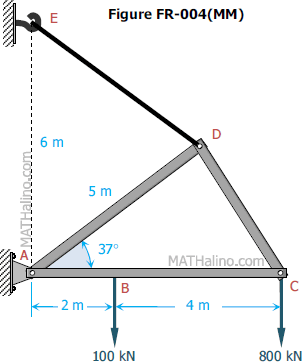
Problem 004-mm | Method of Members
Problem 004-mm
For the structure shown in Fig. FR-004(MM), members AD, DC, and ABC are assumed to be solid rigid members; member ED is a cable. For this structure, determine the reaction at A, the tension on cable ED, and the force in member DC.
- Read more about Problem 004-mm | Method of Members
- Log in or register to post comments
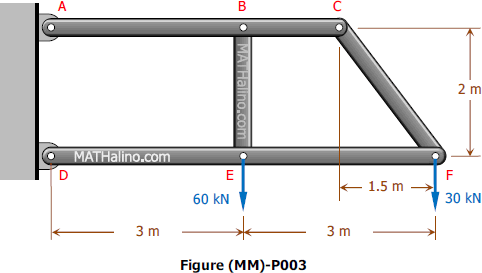
Problem 003-mm | Method of Members
Problem 003-mm
For the structure shown in Fig. (MM)-P003 below, determine the reactions at A and D and the internal force in member CF.
- Read more about Problem 003-mm | Method of Members
- Log in or register to post comments
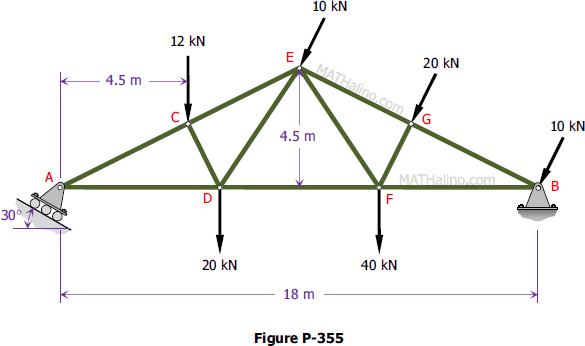
Problem 355 | Equilibrium of Non-Concurrent Force System
Problem 355
Determine the reactions at A and B on the Fink truss shown in Fig. P-355. Members CD and FG are respectively perpendicular to AE and BE at their midpoints.
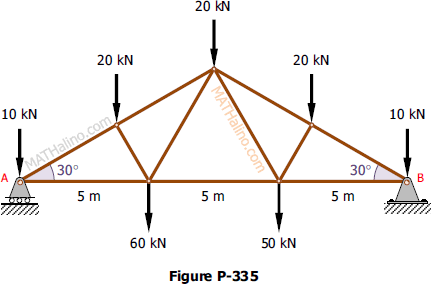
Problem 335 | Equilibrium of Parallel Force System
Problem 335
The roof truss in Fig. P-335 is supported by a roller at A and a hinge at B. Find the values of the reactions.
- Read more about Problem 335 | Equilibrium of Parallel Force System
- Log in or register to post comments
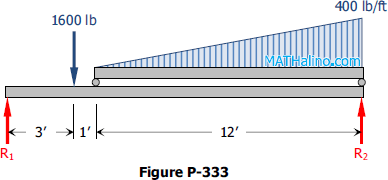
Problem 333 | Equilibrium of Parallel Force System
Problem 333
Determine the reactions R1 and R2 of the beam in Fig. P-333 loaded with a concentrated load of 1600 lb and a load varying from zero to an intensity of 400 lb per ft.
- Read more about Problem 333 | Equilibrium of Parallel Force System
- Log in or register to post comments