Problem 658 | Beam Deflection by Conjugate Beam Method
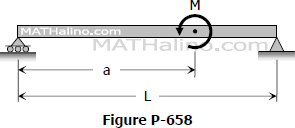
Problem 658
For the beam shown in Fig. P-658, find the value of EIδ at the point of application of the couple.
- Read more about Problem 658 | Beam Deflection by Conjugate Beam Method
- Log in or register to post comments
Problem 657 | Beam Deflection by Conjugate Beam Method
Problem 657
Determine the midspan value of EIδ for the beam shown in Fig. P-657.
- Read more about Problem 657 | Beam Deflection by Conjugate Beam Method
- Log in or register to post comments
Problem 656 | Beam Deflection by Conjugate Beam Method
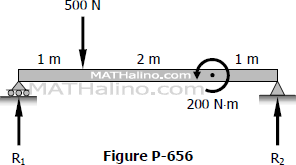
Problem 656
Find the value of EIδ at the point of application of the 200 N·m couple in Fig. P-656.
- Read more about Problem 656 | Beam Deflection by Conjugate Beam Method
- Log in or register to post comments
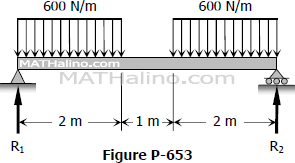
Problem 655 | Beam Deflection by Conjugate Beam Method
Problem 655
Find the value of EIδ under each concentrated load of the beam shown in Fig. P-655.
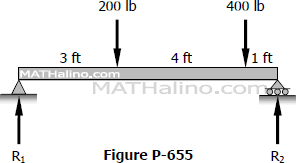
Problem 654 | Beam Deflection by Conjugate Beam Method
Problem 654
For the beam in Fig. P-654, find the value of EIδ at 2 ft from R2.
- Read more about Problem 654 | Beam Deflection by Conjugate Beam Method
- Log in or register to post comments
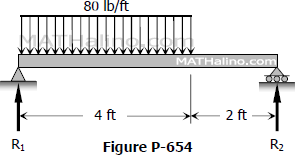
Problem 653 | Beam Deflection by Conjugate Beam Method
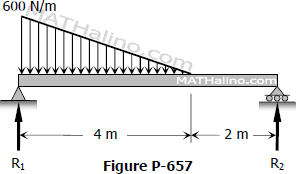
Problem 653
Compute the midspan value of EIδ for the beam shown in Fig. P-653. (Hint: Draw the M diagram by parts, starting from midspan toward the ends. Also take advantage of symmetry.
- Read more about Problem 653 | Beam Deflection by Conjugate Beam Method
- Log in or register to post comments
Conjugate Beam Method | Beam Deflection
Deflection on real beam = Moment on conjugate beam
Properties of Conjugate Beam
Engr. Christian Otto Mohr
- The length of a conjugate beam is always equal to the length of the actual beam.
- The load on the conjugate beam is the M/EI diagram of the loads on the actual beam.
- Read more about Conjugate Beam Method | Beam Deflection
- Log in or register to post comments
Solution to Problem 665 | Deflections in Simply Supported Beams
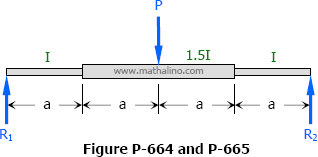
Problem 665
Replace the concentrated load in Prob. 664 by a uniformly distributed load of intensity wo acting over the middle half of the beam. Find the maximum deflection.
Solution to Problem 664 | Deflections in Simply Supported Beams
Problem 664
The middle half of the beam shown in Fig. P-664 has a moment of inertia 1.5 times that of the rest of the beam. Find the midspan deflection. (Hint: Convert the M diagram into an M/EI diagram.)
