Length of one side for maximum area of trapezoid (solution by Calculus)
Problem
BC of trapezoid ABCD is tangent at any point on circular arc DE whose center is O. Find the length of BC so that the area of ABCD is maximum.
Maxima and Minima
55 - Greatest angle subtended by a picture
Problem 55
The lower edge of the picture is a ft, the upper edge is b ft, above the eye of an observer. At what horizontal distance should he stand, if the vertical angle subtended by the picture is to be greatest?
- Read more about 55 - Greatest angle subtended by a picture
- Log in to post comments
Problems in Caculus Involving Inverse Trigonometric Functions
The following are problems involving inverse trigonometric functions.
26-27 Horizontal rod entering into a room from a perpendicular corridor
Problem 26
A corridor 4 ft wide opens into a room 100 ft long and 32 ft wide, at the middle of one side. Find the length of the longest thin rod that can be carried horizontally into the room.
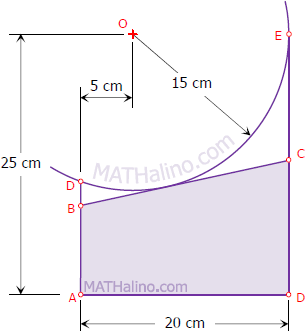
24-25 Largest rectangle inscribed in a circular quadrant
Problem 24
Find the area of the largest rectangle that can be cut from a circular quadrant as in Fig. 76.
23 - Sphere cut into a pyramid
Problem 23
A sphere is cut in the form of a right pyramid with a square base. How much of the material can be saved?
- Read more about 23 - Sphere cut into a pyramid
- Log in to post comments
22 - Smallest cone that may circumscribe a sphere
Problem 22
A sphere of radius a is dropped into a conical vessel full of water. Find the altitude of the smallest cone that will permit the sphere to be entirely submerged.
20-21 Width of the second corridor for a pole to pass horizontally
Problem 20
A pole 24 feet long is carried horizontally along a corridor 8 feet wide and into a second corridor at right angles to the first. How wide must the second corridor be?
Problem 21
Solve Problem 20 if the pole is of length $L$ and the first corridor is of width $C$.
19 Direction of the man to reach his destination as soon as possible
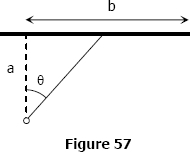Problem 19
A man on an island a miles south of a straight beach wishes to reach a point on shore b miles east of his present position. If he can row r miles per hour and walk w miles per hour, in what direction should he row, to reach his destination as soon as possible? See Fig. 57.
17-18 A man in a motorboat needs to catch a bus
Problem 17
A man in a motorboat at A receives a message at noon, calling him to B. A bus making 40 miles per hour leaves C, bound for B, at 1:00 PM. If AC = 30 miles, what must be the speed of the boat, to enable the man to catch the bus?