flexural stress | MATHalino reviewer about flexural stress

Problem 530
Repeat Prob. 529 if the distributed load is 12 kN/m and the length of the beam is 8 m.

General instruction

Assume that the beam in the problem is properly braced against lateral deflection. Be sure to include the weight of the beam itself.

Read more about Solution to Problem 530 | Economic Sections
Log in or register to post comments

Read more about Solution to Problem 529 | Economic Sections
Log in or register to post comments

Problem 527
In Prob. 526, if the load on the overhang is 600 lb/ft and the overhang is x ft long, find the maximum values of P and x that can be used simultaneously.

Read more about Solution to Problem 527 | Flexure Formula
Log in or register to post comments

Problem 526
A wood beam 6 in wide by 12 in deep is loaded as shown in Fig. P-526. If the maximum flexural stress is 1200 psi, find the maximum values of w_o and P which can be applied simultaneously?

Read more about Solution to Problem 526 | Flexure Formula
Log in or register to post comments

Problem 525
A square timber beam used as a railroad tie is supported by a uniformly distributed loads and carries two uniformly distributed loads each totaling 48 kN as shown in Fig. P-525. Determine the size of the section if the maximum stress is limited to 8 MPa.

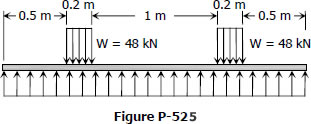
Read more about Solution to Problem 525 | Flexure Formula
Log in or register to post comments

Problem 524
A beam with an S380 × 74 section carries a total uniformly distributed load of 3W and a concentrated load W, as shown in Fig. P-524. Determine W if the flexural stress is limited to 120 MPa.

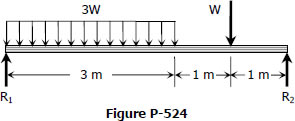
Read more about Solution to Problem 524 | Flexure Formula
Log in or register to post comments

Problem 523
Solve Prob. 522 if w_o = 600 lb/ft.

Read more about Solution to Problem 523 | Flexure Formula
Log in or register to post comments

Problem 522
A box beam is composed of four planks, each 2 inches by 8 inches, securely spiked together to form the section shown in Fig. P-522. Show that I_NA = 981.3 in⁴. If w_o = 300 lb/ft, find P to cause a maximum flexural stress of 1400 psi.

Read more about Solution to Problem 522 | Flexure Formula
Log in or register to post comments

Problem 521
A beam made by bolting two C10 × 30 channels back to back, is simply supported at its ends. The beam supports a central concentrated load of 12 kips and a uniformly distributed load of 1200 lb/ft, including the weight of the beam. Compute the maximum length of the beam if the flexural stress is not to exceed 20 ksi.

Read more about Solution to Problem 521 | Flexure Formula
Log in or register to post comments

Problem 520
A beam with an S310 × 74 section (see Appendix B of textbook) is used as a simply supported beam 6 m long. Find the maximum uniformly distributed load that can be applied over the entire length of the beam, in addition to the weight of the beam, if the flexural stress is not to exceed 120 MPa.

Read more about Solution to Problem 520 | Flexure Formula
Log in or register to post comments