centroid

Problem 715
Determine the coordinates of the centroid of the area shown in Fig. P-715 with respect to the given axes.
 

Problem 714
The dimensions of the T-section of a cast-iron beam are shown in Fig. P-714. How far is the centroid of the area above the base?
 

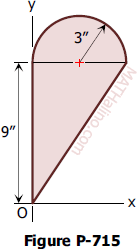
Problem 709
Locate the centroid of the area bounded by the x-axis and the sine curve $y = a \sin \dfrac{\pi x}{L}$ from x = 0 to x = L.
 

Problem 708
Compute the area of the spandrel in Fig. P-708 bounded by the x-axis, the line x = b, and the curve y = kxⁿ where n ≥ 0. What is the location of its centroid from the line x = b? Determine also the y coordinate of the centroid.
 

Problem 707
Determine the centroid of the quadrant of the ellipse shown in Fig. P-707. The equation of the ellipse is $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$.
 

Problem 706
Determine the centroid of the quarter circle shown in Fig. P-706 whose radius is r.
 

Problem 705
Determine the centroid of the shaded area shown in Fig. P-705, which is bounded by the x-axis, the line x = a and the parabola y² = kx.
 

Problem 240
The shaded area in Fig P-240 represents a steel plate of uniform thickness. A hole of 4-in. diameter has been cut in the plate. Locate the center of gravity the plate. Hint: The weight of the plate is equivalent to the weight of the original plate minus the weight of material cut away. Represent the original plate weight of plate by a downward force acting at the center of the 10 × 14 in. rectangle. Represent the weight of the material cut away by an upward force acting at the center of the circle. Locate the position of the resultant of these two forces with respect to the left edge and bottom of the plate.
 

This page will define the following: incenter, circumcenter, orthocenter, centroid, and Euler line.
 

Incenter
Incenter is the center of the inscribed circle (incircle) of the triangle, it is the point of intersection of the angle bisectors of the triangle.
 

The radius of incircle is given by the formula

where A_t = area of the triangle and s = ½ (a + b + c). See the derivation of formula for radius of incircle.