Solution to Problem 350 | Helical Springs
Problem 350
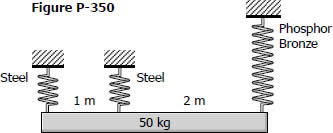
As shown in Fig. P-350, a homogeneous 50-kg rigid block is suspended by the three springs whose lower ends were originally at the same level. Each steel spring has 24 turns of 10-mm-diameter on a mean diameter of 100 mm, and G = 83 GPa. The bronze spring has 48 turns of 20-mm-diameter wire on a mean diameter of 150 mm, and G = 42 GPa. Compute the maximum shearing stress in each spring using Eq. (3-9).
- Read more about Solution to Problem 350 | Helical Springs
- Log in or register to post comments




