Active forum topics
- Hydraulics: Rotating Vessel
- Inverse Trigo
- Application of Differential Equation: Newton's Law of Cooling
- Problems in progression
- General Solution of $y' = x \, \ln x$
- engineering economics: construct the cash flow diagram
- Eliminate the Arbitrary Constants
- Law of cosines
- Maxima and minima (trapezoidal gutter)
- Special products and factoring
New forum topics
- Hydraulics: Rotating Vessel
- Inverse Trigo
- Problems in progression
- General Solution of $y' = x \, \ln x$
- engineering economics: construct the cash flow diagram
- Integration of 4x^2/csc^3x√sinxcosx dx
- Maxima and minima (trapezoidal gutter)
- Special products and factoring
- Newton's Law of Cooling
- Find the roots of the quadratic equation by differentiation method
Recent comments
- Bakit po nagmultiply ng 3/4…3 weeks 3 days ago
- Determine the least depth…10 months 3 weeks ago
- Solve mo ang h manually…3 weeks 3 days ago
- Paano kinuha yung height na…11 months ago
- It's the unit conversion…11 months 2 weeks ago
- Refer to the figure below…11 months 1 week ago
- where do you get the sqrt413 weeks 3 days ago
- Thank you so much3 weeks 2 days ago
- How did you get the 2.8 mins…3 weeks 2 days ago
- How did you get the distance…3 weeks 2 days ago
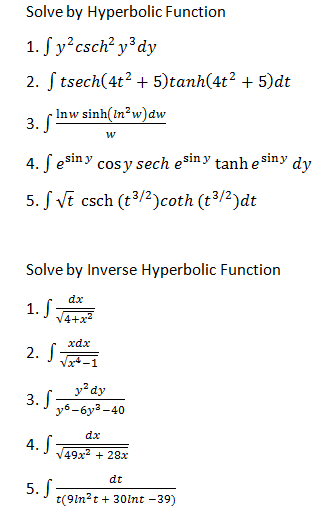
Re: patulong po Hyperbolic and Inverse Hyperbolic functions...
Number 1
$\displaystyle \int y^2 \, {\rm csch} \, y^3 \, dy$
$\displaystyle = \frac{1}{3} \int {\rm csch} \, y^3 (3y^2\, dy)$
$\displaystyle = -\frac{1}{3} {\rm coth} \, y^3 + C$