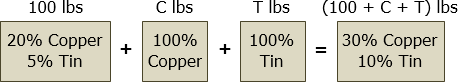Problem
A given alloy contains 20% copper and 5% tin. How many pounds of copper and of tin must be melted with 100 lb of the given alloy to produce another alloy analyzing 30% copper and 10% tin? All percentages are by weight.
Problem
A nutritionist in a hospital is arranging special diets that consist of a combination of three basic foods. It is important that the patients on this diet consume exactly 310 units of calcium, 190 units of iron, and 250 units of vitamin A each day. The amounts of these nutrients in one ounce food are given in the following table.
| Units Per Ounce | |||
| Calcium | Iron | Vitamin A | |
| Food A | 30 | 10 | 10 |
| Food B | 10 | 10 | 30 |
| Food C | 20 | 20 | 20 |
How many ounces each food must be used to satisfy the nutrient requirements exactly?
Situation
A temporary earth retaining wall consists of wooden plank driven vertically into the ground. The wall is designed to resist 2.4 m height of soil.
1. Calculate the maximum flexural stress.
| A. 12.7 MPa | C. 8.6 MPa |
| B. 14.2 MPa | D. 10.1 MPa |
2. Calculate the maximum shear stress.
| A. 1.11 MPa | C. 0.99 MPa |
| B. 0.33 MPa | D. 0.77 MPa |
3. Calculate the minimum thickness of the plank to prevent failure.
| A. 90 mm | C. 110 mm |
| B. 80 mm | D. 100 mm |
Problem
A catapult is placed 100 ft from the castle wall, which is 35 feet high. The soldier wants the burning bale of hay to clear the top of the wall and land 50 feet inside the castle wall. If the initial velocity of the bale is 70 feet per second, then at what angle should the bale of hay be launched so that it travel 150 feet and pass over the castle wall. Use g = 32 ft/sec2.
| A. 49.8° | C. 39.2° |
| B. 50.8° | D. 40.2° |
Problem
A parabola has an equation of y2 = 8x. Find the equation of the diameter of the parabola, which bisect chords parallel to the line x – y = 4.
| A. y = 2 | C. y = 4 |
| B. y = 3 | D. y = 1 |
Situation
Diagonals BG, CF, CH, and DG of the truss shown can resist tension only.
If W = 3 kN and P = 0, find the following:
1. the force in member CF.
| A. 4.76 kN | C. 4.67 kN |
| B. 4.32 kN | D. 4.23 kN |
2. the force in member BF.
| A. 3.2 kN | C. 3.4 kN |
| B. 3.3 kN | D. 3.5 kN |
3. the force in member DH.
| A. 2.8 kN | A. 2.5 kN |
| B. 2.8 kN | D. 2.7 kN |
Situation
Flexible cables BE and CD are used to brace the truss shown below.
1. Determine the load W to cause a compression force of 8.9 kN to member BD.
| A. 7.80 kN | C. 26.70 kN |
| B. 35.64 kN | D. 13.35 kN |
2. Which cable is in tension and what is the tensile reaction?
| A. BE = 12.58 kN | C. BE = 6.29 kN |
| B. CD = 6.29 kN | D. CD = 12.58 kN |
3. If W = 20 kN, what will be the tensile reaction of member CE?
| A. 6.67 kN | C. 0 |
| B. 13.33 kN | D. 10 kN |
Problem
Determine the absolute pressure in a vessel of mercury at a point 200 mm below its surface.
| A. 126 kPa | C. 128 kPa |
| B. 130 kPa | D. 132 kPa |
Problem
Given the Fourier equation:
$$f(t) = 5 \cos (20\pi t) + 2 \cos (40\pi t + \cos (80\pi t)$$
What is the fundamental frequency?
| A. 10 | C. 40 |
| B. 20 | D. 30 |
Problem
A salesperson earns P60,000 per month plus a commission of 20% of sales. Find the minimum amount of sales needed to receive a total income of at least P150,000 per month.
| A. P150,000 | C. P450,000 |
| B. P350,000 | D. P250,000 |
