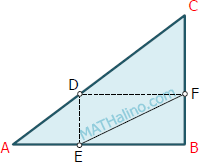
Distance between projection points on the legs of right triangle (solution by Calculus)
Problem
From the right triangle ABC shown below, AB = 40 cm and BC = 30 cm. Points E and F are projections of point D from hypotenuse AC to the perpendicular legs AB and BC, respectively. How far is D from AB so that length EF is minimal?
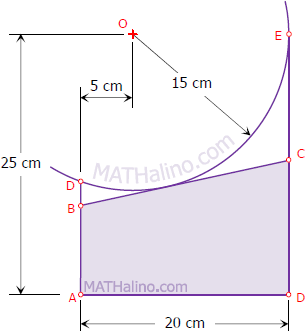
Length of one side for maximum area of trapezoid (solution by Geometry)
Problem
BC of trapezoid ABCD is tangent at any point on circular arc DE whose center is O. Find the length of BC so that the area of ABCD is maximum.
Quadrilateral Circumscribing a Circle
Quadrilateral circumscribing a circle (also called tangential quadrilateral) is a quadrangle whose sides are tangent to a circle inside it.
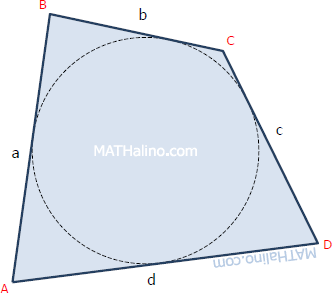
Area,
$A = rs$
Where r = radius of inscribed circle and s = semi-perimeter = (a + b + c + d)/2
Derivation for area
- Read more about Quadrilateral Circumscribing a Circle
- Log in or register to post comments
Common Quadrilaterals
Square
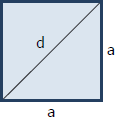
Area, $A = a^2$
Perimeter, $P = 4a$
Diagonal, $d = a\sqrt{2}$
- Read more about Common Quadrilaterals
- Log in or register to post comments