May 2012

Problem
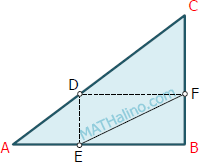
From the right triangle ABC shown below, AB = 40 cm and BC = 30 cm. Points E and F are projections of point D from hypotenuse AC to the perpendicular legs AB and BC, respectively. How far is D from AB so that length EF is minimal?
 

Problem
From the figure shown, ABC and DEF are equilateral triangles. Point E is the midpoint of AC and points D and F are on the circle circumscribing ABC. If AB is 12 cm, find DE.
 

Problem
The figure shown below is a square of side 4 inches. Line rays are drawn from each corner of the square to the midpoints of the opposite sides. Find the area of the shaded region.
 

Problem
Three squares are drawn so that each will contain a side of regular hexagon as shown in the given figure. If the hexagon has a perimeter of 60 in., compute the area of the region common to the three squares. The required area is the shaded region in the figure.
 

Problem
From the figure shown, AB = diameter of circle O₁ = 30 cm, BC = diameter of circle O₂ = 40 cm, and AC = diameter of circle O₃ = 50 cm. Find the shaded areas A₁, A₂, A₃, and A₄ and check that A₁ + A₂ + A₃ = A₄ as stated in the previous problem.
 

Problem
From the figure shown below, O₁, O₂, and O₃ are centers of circles located at the midpoints of the sides of the triangle ABC. The sides of ABC are diameters of the respective circles. Prove that
 

where A₁, A₂, A₃, and A₄ are areas in shaded regions.
 

Problem 719
Determine the centroid of the lines that form the boundary of the shaded area in Fig. P-718.
 

Problem 718
Locate the centroid of the shaded area shown in Fig. P-718.
 

Problem 717
Locate the centroid of the bent wire shown in Fig. P-717. The wire is homogeneous and of uniform cross-section.
 

Problem 716
A slender homogeneous wire of uniform cross section is bent into the shape shown in Fig. P-716. Determine the coordinates of the centroid.