February 2009

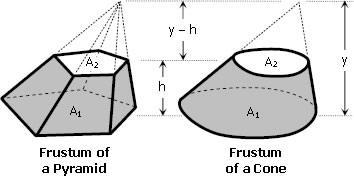
Frustum of a pyramid and frustum of a cone
 

The formula for frustum of a pyramid or frustum of a cone is given by
 

Where:
h = perpendicular distance between A₁ and A₂ (h is called the altitude of the frustum)
A₁ = area of the lower base
A₂ = area of the upper base
Note that A₁ and A₂ are parallel to each other.
 

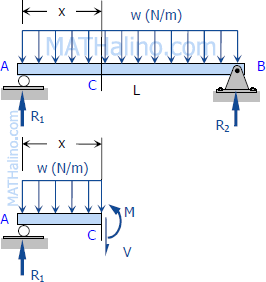The vertical shear at C in the figure shown in previous section (also shown to the right) is taken as
$V_C = (\Sigma F_v)_L = R_1 - wx$
 

where R₁ = R₂ = wL/2
 

$V_c = \dfrac{wL}{2} - wx$
 

The moment at C is
$M_C = (\Sigma M_C) = \dfrac{wL}{2}x - wx \left( \dfrac{x}{2} \right)$

$M_C = \dfrac{wLx}{2} - \dfrac{wx^2}{2}$
 

If we differentiate M with respect to x:
$\dfrac{dM}{dx} = \dfrac{wL}{2} \cdot \dfrac{dx}{dx} - \dfrac{w}{2} \left( 2x \cdot \dfrac{dx}{dx} \right)$

$\dfrac{dM}{dx} = \dfrac{wL}{2} - wx = \text{shear}$
 

thus,

Problem 422
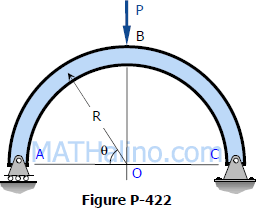
Write the shear and moment equations for the semicircular arch as shown in Fig. P-422 if (a) the load P is vertical as shown, and (b) the load is applied horizontally to the left at the top of the arch.
 

Problem 421
Write the shear and moment equations as functions of the angle θ for the built-in arch shown in Fig. P-421.