Solution to Problem 349 | Helical Springs
Problem 349
A rigid bar, hinged at one end, is supported by two identical springs as shown in Fig. P-349. Each spring consists of 20 turns of 10-mm wire having a mean diameter of 150 mm. Compute the maximum shearing stress in the springs, using Eq. (3-9). Neglect the mass of the rigid bar.
- Read more about Solution to Problem 349 | Helical Springs
- Log in or register to post comments
Solution to Problem 348 | Helical Springs
Problem 348
A rigid bar, pinned at O, is supported by two identical springs as shown in Fig. P-348. Each spring consists of 20 turns of 3/4-in-diameter wire having a mean diameter of 6 in. Determine the maximum load W that may be supported if the shearing stress in the springs is limited to 20 ksi. Use Eq. (3-9).
- Read more about Solution to Problem 348 | Helical Springs
- 1 comment
- Log in or register to post comments
Solution to Problem 347 | Helical Springs
Problem 347
Two steel springs arranged in series as shown in Fig. P-347 supports a load P. The upper spring has 12 turns of 25-mm-diameter wire on a mean radius of 100 mm. The lower spring consists of 10 turns of 20-mm diameter wire on a mean radius of 75 mm. If the maximum shearing stress in either spring must not exceed 200 MPa, compute the maximum value of P and the total elongation of the assembly. Use Eq. (3-10) and G = 83 GPa. Compute the equivalent spring constant by dividing the load by the total elongation.
- Read more about Solution to Problem 347 | Helical Springs
- Log in or register to post comments
Solution to Problem 346 | Helical Springs
Problem 346
Compute the maximum shearing stress developed in a phosphor bronze spring having mean diameter of 200 mm and consisting of 24 turns of 20-mm diameter wire when the spring is stretched 100 mm. Use Eq. (3-10) and G = 42 GPa.
- Read more about Solution to Problem 346 | Helical Springs
- 1 comment
- Log in or register to post comments
Solution to Problem 345 | Helical Springs
Problem 345
A helical spring is fabricated by wrapping wire 3/4 in. in diameter around a forming cylinder 8 in. in diameter. Compute the number of turns required to permit an elongation of 4 in. without exceeding a shearing stress of 18 ksi. Use Eq. (3-9) and G = 12 × 106 psi.
- Read more about Solution to Problem 345 | Helical Springs
- 1 comment
- Log in or register to post comments
Solution to Problem 344 | Helical Springs
Problem 344
Determine the maximum shearing stress and elongation in a bronze helical spring composed of 20 turns of 1.0-in.-diameter wire on a mean radius of 4 in. when the spring is supporting a load of 500 lb. Use Eq. (3-10) and G = 6 × 106 psi.
- Read more about Solution to Problem 344 | Helical Springs
- Log in or register to post comments
Solution to Problem 343 | Helical Springs
Problem 343
Determine the maximum shearing stress and elongation in a helical steel spring composed of 20 turns of 20-mm-diameter wire on a mean radius of 90 mm when the spring is supporting a load of 1.5 kN. Use Eq. (3-10) and G = 83 GPa.
- Read more about Solution to Problem 343 | Helical Springs
- Log in or register to post comments
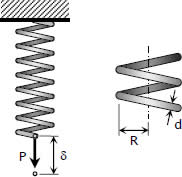
Helical Springs
When close-coiled helical spring, composed of a wire of round rod of diameter d wound into a helix of mean radius R with n number of turns, is subjected to an axial load P produces the following stresses and elongation:
The maximum shearing stress is the sum of the direct shearing stress τ1 = P/A and the torsional shearing stress τ2 = Tr/J, with T = PR.
- Read more about Helical Springs
- Log in or register to post comments
Solution to Problem 341 | Torsion of thin-walled tube
Problem 341
Derive the torsion formula τ = Tρ / J for a solid circular section by assuming the section is composed of a series of concentric thin circular tubes. Assume that the shearing stress at any point is proportional to its radial distance.
- Read more about Solution to Problem 341 | Torsion of thin-walled tube
- Log in or register to post comments