016 Radius of the sphere circumscribing a regular triangular pyramid
Example 016
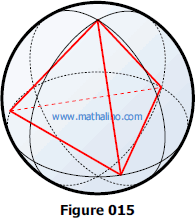
Find the area of the surface and the volume of the sphere circumscribed about a regular tetrahedron of edge 25 cm. See Figure 015.
Volume of the Sphere
015 Two unequal balls inside the cylinder
Example 015
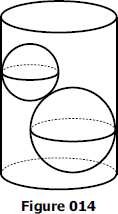
Two balls, one 15 cm in diameter and the other 10 cm in diameter, are placed in a cylindrical jar 20 cm in diameter, as shown in Figure 014. Find the volume of water necessary to cover them.
- Read more about 015 Two unequal balls inside the cylinder
- Log in or register to post comments
014 Water poured into a jar of marbles
Example 014
A boy who had discovered that 20 mm marbles fitted snugly into the bottom of a cylindrical jar, dropped in a fourth on top of the three and poured water enough into the jar to just cover them. How much water did he use?
- Read more about 014 Water poured into a jar of marbles
- Log in or register to post comments
013 Insciribed and circumscribed sphere about a cube - volume comparison
Example 013
Compare the volume of a sphere inscribed in a cube with volume of the sphere that circumscribes the cube.
012 Sphere circumscribed about a right circular cylinder
Example 012
Find the volume and total area of the sphere which circumscribes a cylinder of revolution whose altitude and diameter are each 6 inches.
007 - 008 Volume and surface area of earth and balloon
Example 007
A spherical balloon is inflated so that so that its diameter is 12 m. Find the surface area of the balloon’s covering and the volume of the gas.
- Read more about 007 - 008 Volume and surface area of earth and balloon
- Log in or register to post comments
005 Weight of ivory billiard balls
Example 005
A cubic foot of ivory weighs 114 lb. Find the weight of 1000 ivory billiard balls 2½ inch in diameter.
- Read more about 005 Weight of ivory billiard balls
- Log in or register to post comments
003 Weight of an iron shell
Example 003
An iron ball 10 cm in diameter weighs 4 kg. Find the weight of an iron shell 5 cm thick whose external diameter is 50 cm.
- Read more about 003 Weight of an iron shell
- Log in or register to post comments
002 Weight of snow ball
Problem 002
Find the weight of the snowball 1.2 m in diameter if the wet compact snow of which this ball is made weighs 480 kg/m3
- Read more about 002 Weight of snow ball
- Log in or register to post comments
001 Solid steel ball remolded into hollow steel ball
Problem 001
A 523.6 cm3 solid spherical steel ball was melted and remolded into a hollow steel ball so that the hollow diameter is equal to the diameter of the original steel ball. Find the thickness of the hollow steel ball.
- Read more about 001 Solid steel ball remolded into hollow steel ball
- Log in or register to post comments