Uniformly Distributed Load
Problem 824 | Continuous Beam by Three-Moment Equation
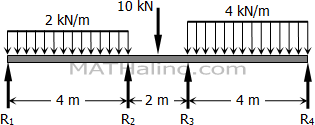
Problem 824
The first span of a simply supported continuous beam is 4 m long, the second span is 2 m long and the third span is 4 m long. Over the first span there is a uniformly distributed load 2 kN/m, and over the third span there is a uniformly distributed load of 4 kN/m. At the midpoint of the second span, there is a concentrated load of 10 kN. Solve for the moment over the supports and check your answers using Problems 820 and 821.
Problem 822 | Continuous Beam by Three-Moment Equation
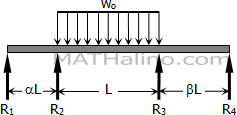
Problem 822
Solve Prob. 821 if the concentrated load is replaced by a uniformly distributed load of intensity wo over the middle span.
Answers:
$M_2 = -\dfrac{w_o L^2}{4} \cdot \dfrac{1 + 2\beta}{4(\alpha + 1)(1 + \beta) - 1}$
$M_3 = -\dfrac{w_o L^2}{4} \cdot \dfrac{1 + 2\alpha}{4(1 + \alpha)(1 + \beta) - 1}$
Problem 820 | Continuous Beam by Three-Moment Equation
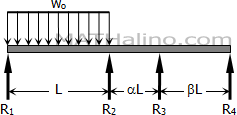
Problem 820
Solve Prob. 819 if the concentrated load is replaced by a uniformly distributed load of intensity wo over the first span.
Problem 1007 | Flexural stresses developed in the wood and steel fibers
Problem 1007
A uniformly distributed load of 300 lb/ft (including the weight of the beam) is simply supported on a 20-ft span. The cross section of the beam is described in Problem 1005. If n = 20, determine the maximum stresses produced in the wood and the steel.
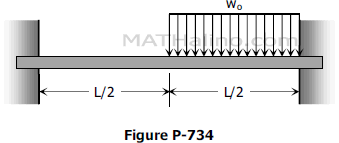
Problem 734 | Restrained beam with uniform load over half the span
Problem 734
Determine the end moments for the restrained beams shown in Fig. P-734.
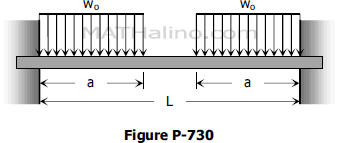
Problem 730 | Uniform loads at each end of fully restrained beam
Problem 703
Determine the end moment and maximum deflection for a perfectly restrained beam loaded as shown in Fig. P-730.