Truss

Problem 004-ms
For the truss shown in Fig. T-05, find the internal fore in member BE.
 

Problem 003-mj
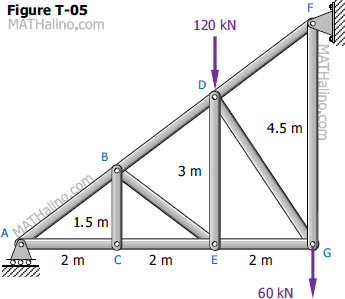
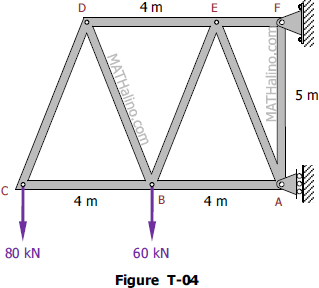
Find the force in each member of the truss shown in Fig. T-04.
 

Problem 003-ms
The truss in Fig. T-04 is pinned to the wall at point F, and supported by a roller at point C. Calculate the force (tension or compression) in members BC, BE, and DE.
 

Figure T-04

Problem 002-ms
The roof truss shown in Fig. T-03 is pinned at point A, and supported by a roller at point H. Determine the force in member DG.
 

Problem 002-mj
The structure in Fig. T-02 is a truss which is pinned to the floor at point A, and supported by a roller at point D. Determine the force to all members of the truss.
 

Problem 001-ms
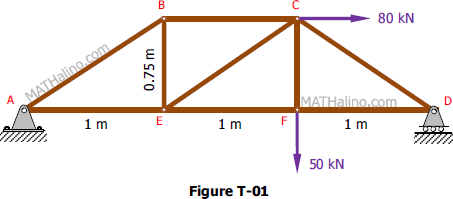
From the truss in Fig. T-01, determine the force in mebers BC, CE, and EF.
 

Problem 403
Determine the force in each bar of the truss shown in Fig. P-403.
 

Problem
Find the force acting in all members of the truss shown in Figure T-01.
 

Method of Joints
The free-body diagram of any joint is a concurrent force system in which the summation of moment will be of no help. Recall that only two equilibrium equations can be written
 

There are many kinds of structure. This section will limit to those that are pin-connected. Two types of pin-connected structures will be covered here; pin-connected trusses and pin-connected frames. In the actual structure, the joints may be welded, riveted, or bolted to a gusset plate at the joint. However as long as the center-line of the member coincide at the joint, the assumption of a pinned joint maybe used.