simple beam

The slope or deflection at any point on the beam is equal to the resultant of the slopes or deflections at that point caused by each of the load acting separately.
 

Problem 681
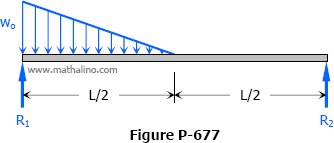
Show that the midspan value of EIδ is (w_ob/48)(L³ - 2Lb² + b³) for the beam in part (a) of Fig. P-681. Then use this result to find the midspan EIδ of the loading in part (b) by assuming the loading to exceed over two separate intervals that start from midspan and adding the results.
 

Problem 680
Determine the midspan value of EIδ for the beam loaded as shown in Fig. P-680.
 

Problem 679
Determine the midspan value of EIδ for the beam shown in Fig. P-679 that carries a uniformly varying load over part of the span.
 

Problem 678
Determine the midspan value of EIδ for the beam shown in Fig. P-678.
 

Problem 677
Determine the midspan deflection of the beam loaded as shown in Fig. P-677.
 

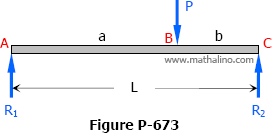
Problem 673
For the beam shown in Fig. P-673, show that the midspan deflection is δ = (Pb/48EI) (3L² - 4b²).
 

Problem 665
Replace the concentrated load in Prob. 664 by a uniformly distributed load of intensity w_o acting over the middle half of the beam. Find the maximum deflection.