concentrated load

Problem 656
Find the value of EIδ at the point of application of the 200 N·m couple in Fig. P-656.
 

Problem 655
Find the value of EIδ under each concentrated load of the beam shown in Fig. P-655.
 

Problem 643
Find the maximum value of EIδ for the cantilever beam shown in Fig. P-643.
 

Problem 641
For the cantilever beam shown in Fig. P-641, what will cause zero deflection at A?
 

Problem 640
Compute the value of δ at the concentrated load in Prob. 639. Is the deflection upward downward?
 

Problem 639
The downward distributed load and an upward concentrated force act on the cantilever beam in Fig. P-639. Find the amount the free end deflects upward or downward if E = 1.5 × 10⁶ psi and I = 60 in⁴.
 

Problem 636
The cantilever beam shown in Fig. P-636 has a rectangular cross-section 50 mm wide by h mm high. Find the height h if the maximum deflection is not to exceed 10 mm. Use E = 10 GPa.
 

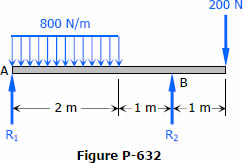
Problem 632
For the beam loaded as shown in Fig. P-632, compute the value of (Area_AB) barred(X)_A. From this result, is the tangent drawn to the elastic curve at B directed up or down to the right? (Hint: Refer to the deviation equations and rules of sign.)
 

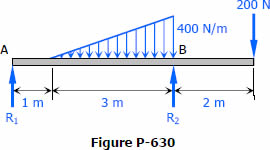
Problem 630
For the beam loaded as shown in Fig. P-630, compute the value of (Area_AB)barred(X)_A . From the result determine whether the tangent drawn to the elastic curve at B slopes up or down to the right. (Hint: Refer to the deviation equations and rules of sign.)
 

Problem 625
For the beam loaded as shown in Fig. P-625, compute the moment of area of the M diagrams between the reactions about both the left and the right reaction. (Hint: Draw the moment diagram by parts from right to left.)