If x varies directly as y and inversely as z and x = 14 when y = 7, and z = 2. Find x when y = 16 and z = 4.
If x varies directly as y and inversely as z and x = 14 when y = 7, and z = 2. Find x when y = 16 and z = 4.
December 2020
If z varies directly as x and inversely as the square of y, and z = 1/3, x = 4, and y = 6, find z when x = 12 and y = 4.
If z varies directly as x and inversely as the square of y, and z = 1/3, x = 4, and y = 6, find z when x = 12 and y = 4.
Solid Mensuration: Prismatoid
The altitude of the storage bin shown in the sketch is 12ft and the bases are parallel rectangles having the dimensions indicated. Find the capacity.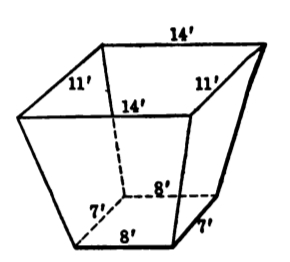 
- Read more about Solid Mensuration: Prismatoid
- 1 comment
- Log in or register to post comments
$\rm \LaTeX$ Code. How to Write an Equation?
All logged in users can include math equations in their posts and it is easy to do. Inline equations can be written between dollar signs and centered equations are between double dollar signs.
Example:
If you write $x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}$ will result to $x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}$. This an example of inline equation. If you wish to center your equation, you can write $$x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$ and it will result to this $$x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$ which is a centered equation.
01 Area of a right triangle of known median bisecting the hypotenuse
Problem
The median of a right triangle drawn to the hypotenuse is 3 cm long and makes an angle of 60° with it. Find the area of the triangle.
| A. 7.97 cm2 | C. 8.79 cm2 |
| B. 8.97 cm2 | D. 7.79 cm2 |
How long will P2.5M amounts to P4.5M at 8% compounded quarterly?
Problem
By the conditions of a will, the sum of P2.5M is left to a girl to be held in a trust fund by her guardian until it amounts to P4.5M. When will the girl receive the money if the fund is invested at 8% compounded quarterly?
| A. 7 years | C. 7.42 years |
| B. 6.8 years | D. 7.25 years |
Length of hypotenuse of a right triangle of known area in the xy-plane
Problem
For triangle BOA, B is on the y-axis, O is the origin, and A is on the x-axis. Point C(5, 2) is on the line AB. Find the length of AB if the area of the triangle is 36 unit2.
| A. 24.31 units | C. 13.42 units |
| B. 18.30 units | D. 10.80 units |
The Straight Line
Definition
Straight line is the locus or path of a point that moves without changing its direction.
General Equation
The general equation of the straight line is given by
$ax + by + c = 0$
- Read more about The Straight Line
- Log in or register to post comments
Differential Equation: $(1-xy)^{-2} dx + \left[ y^2 + x^2 (1-xy)^{-2} \right] dy = 0$
Hello, can anyone solve this equation?
I can't figure it out,
$(1-xy)^{-2} dx + \left[ y^2 + x^2 (1-xy)^{-2} \right] dy = 0$
Thanks.
Differential Equation: $y' = x^3 - 2xy$, where $y(1)=1$ and $y' = 2(2x-y)$ that passes through (0,1)
Can anyone solve this D. E.?
y' = x^3 - 2xy, where y(1)=1
and
y' = 2(2x-y) that passes through (0,1)