Problem 920
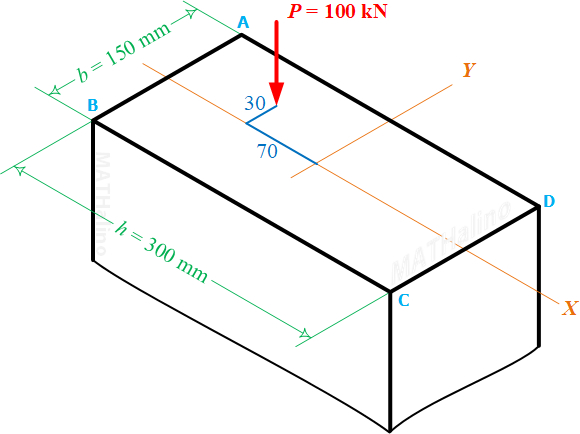
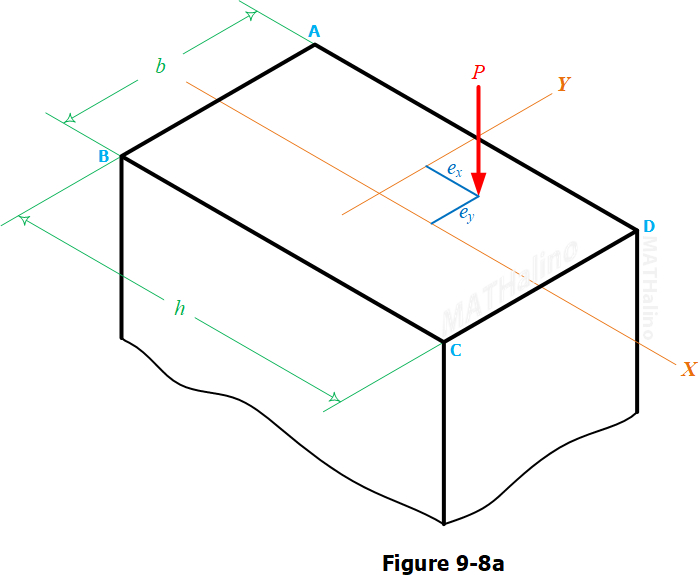
A compressive load P = 100 kN is applied, as shown in Fig. 9-8a, at a point 70 mm to the left and 30 mm above the centroid of a rectangular section for which h = 300 mm and b = 250 mm. What additional load, acting normal to the cross section at its centroid, will eliminate tensile stress anywhere over the cross section?
Problem 919
From the data in Prob. 918, what additional load applied at the centroid is necessary so that no tensile stress will exist anywhere on the cross-section?
Solution 919
Problem 918
A compressive load P = 12 kips is applied, as in Fig. 9-8a, at a point 1 in. to the right and 2 in. above the centroid of a rectangular section for which h = 10 in. and b = 6 in. Compute the stress at each corner and the location of the neutral axis. Illustrate the answers with a sketch.
Consider the cross-section below. A compressive load P is applied at any point (ex, ey) with respect to the principal axes x and y. The moment of P about these axes are respectively
Problem
A rectangular waterfront lot has a perimeter of 1000 feet. To create a sense of privacy, the lot owner decides to fence along three sides excluding the sides that fronts the water. An expensive fencing along the lot’s front length costs Php25 per foot, and an inexpensive fencing along two side widths costs only Php5 per foot. The total cost of the fencing along all three sides comes to Php9500. What is the lot’s dimensions?
| A. 300 feet by 100 feet | C. 400 feet by 200 feet |
| B. 400 feet by 100 feet | D. 300 feet by 200 feet |
Problem
A salesperson earns \$600 per month plus a commission of 20% of sales. Find the minimum amount of sales needed to receive a total income of at least \$1500 per month.
| A. \$1500 | C. \$4500 |
| B. \$3500 | D. \$2500 |
Problem
The tide in Bay of Fundy rises and falls every 13 hours. The depth of the water at a certain point in the bay is modeled by a function d = 5 sin (2π/13)t + 9, where t is time in hours and d is depth in meters. Find the depth at t = 13/4 (high tide) and t = 39/4 (low tide).
Problem
The number of hours daylight, D(t) at a particular time of the year can be approximated by
for t days and t = 0 corresponding to January 1. The constant K determines the total variation in day length and depends on the latitude of the locale. When is the day length the longest, assuming that it is NOT a leap year?
| A. December 20 | C. June 20 |
| B. June 19 | D. December 19 |
Problem
The local weather forecaster says “no rain” and his record is 2/3 accuracy of prediction. But the Federal Meteorological Service predicts rain and their record is 3/4. With no other data available, what is the chance of rain?
| A. 3/5 | C. 1/6 |
| B. 1/4 | D. 5/12 |
Problem
Find the term that is independent of x in the expansion of $\left( 2 + \dfrac{3}{x^2} \right)\left( x - \dfrac{2}{x} \right)^6$.
| A. 180 | C. -140 |
| B. 160 | D. -160 |
