Binomial Theorem
The Expansion of (a + b)n
If $n$ is any positive integer, then
$(a + b)^n = a^n + {_nC_1}a^{n - 1}b + {_nC_2}a^{n - 2}b^2 + \, \cdots \, + {_nC_m}a^{n - m}b^m + \, \cdots \, + b^n$
Where
${_nC_m}$ = combination of n objects taken m at a time.
- Read more about Binomial Theorem
- Log in to post comments
Special Products and Factoring
Special Products
1. $(x + y)(x - y) = x^2 - y^2$
2. $(x + y)^2 = x^2 + 2xy + y^2$
3. $(x - y)^2 = x^2 - 2xy + y^2$
- Read more about Special Products and Factoring
- Log in to post comments
Logarithm and Other Important Properties in Algebra
Properties of Logarithm
- If $y = a^x$, then $\log_a y = x$. ← Definition of logarithm
- $\log_a xy = \log_a x + \log_a y$
- $\log_a \dfrac{x}{y} = \log_a x - \log_a y$
- $\log_a x^n = n \log_a x$
- $\log_a a = 1$
- $\log_a 1 = 0$
- $\log_{10} x = \log x$ ← Common logarithm
- $\log_e x = \ln x$ ← Naperian or natural logarithm
- $\log_y x = \dfrac{\log x}{\log y} = \dfrac{\ln x}{\ln y}$ ← Change base rule
- If $\log_a x = \log_a y$, then $x = y$.
- If $\log_a x = y$, then $x = {\rm antilog}_a \, y$.
Laws of Exponents and Radicals
Laws of Exponents (Index Law)
1. $x^n = x \cdot x \cdot x ... \, (n \text{ factors})$
2. $x^m \cdot x^n = x^{m + n}$
3. $(x^m)^n = x^{mn}$
4. $(xyz)^n = x^n \, y^n \, z^n$
5. $\dfrac{x^m}{x^n} = x^{m - n}$
6. $\left( \dfrac{x}{y} \right)^n = \dfrac{x^n}{y^n}$
7. $x^{-n} = \dfrac{1}{x^n}$ and $\dfrac{1}{x^{-n}} = x^n$
8. $x^0 = 1$, provided $x \ne 0$.
9. $(x^m)^{1/n} = (x^{1/n})^m = x^{m/n}$
10. $x^{m/n} = \sqrt[n]{x^m}$
11. If $x^m = x^n$, then $m = n$ provided $x \ne 0$.
- Read more about Laws of Exponents and Radicals
- Log in to post comments
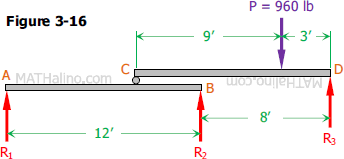
Problem 338 | Equilibrium of Parallel Force System
Problem 338
The two 12-ft beams shown in Fig. 3-16 are to be moved horizontally with respect to each other and load P shifted to a new position on CD so that all three reactions are equal. How far apart will R2 and R3 then be? How far will P be from D?
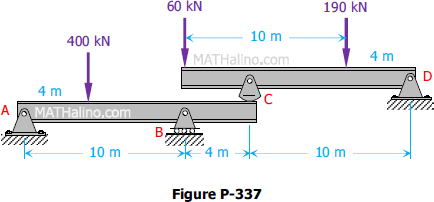
Problem 337 | Equilibrium of Parallel Force System
Problem 337
The upper beam in Fig. P-337 is supported at D and a roller at C which separates the upper and lower beams. Determine the values of the reactions at A, B, C, and D. Neglect the weight of the beams.
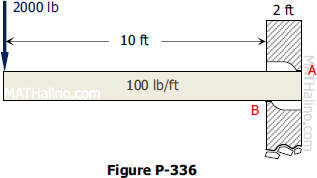
Problem 336 | Equilibrium of Parallel Force System
Problem 336
The cantilever beam shown in Fig. P-336 is built into a wall 2 ft thick so that it rests against points A and B. The beam is 12 ft long and weighs 100 lb per ft.
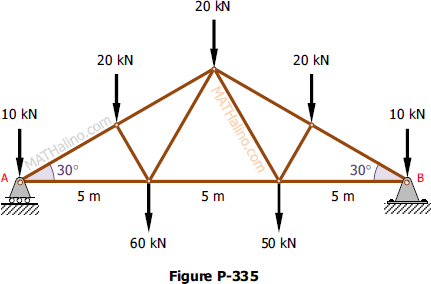
Problem 335 | Equilibrium of Parallel Force System
Problem 335
The roof truss in Fig. P-335 is supported by a roller at A and a hinge at B. Find the values of the reactions.
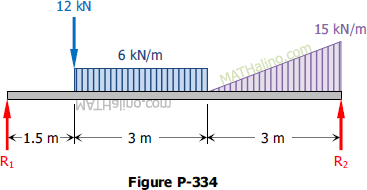
Problem 334 | Equilibrium of Parallel Force System
Problem 334
Determine the reactions for the beam loaded as shown in Fig. P-334.