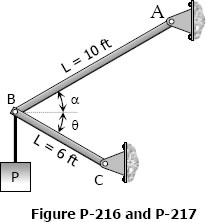
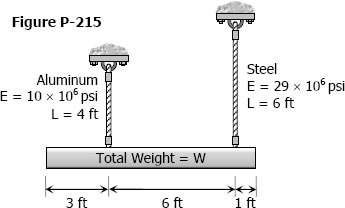
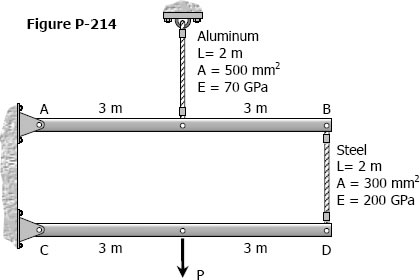
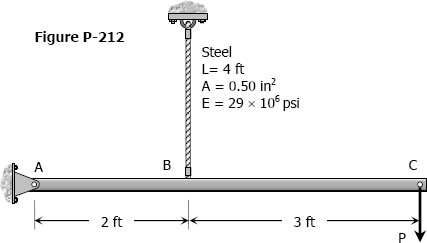
Shearing Deformation

Shearing Deformation
Shearing forces cause shearing deformation. An element subject to shear does not change in length but undergoes a change in shape.
 

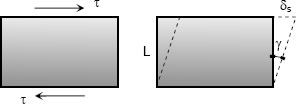
shearing-deformation.jpg

 

The change in angle at the corner of an original rectangular element is called the shear strain and is expressed as
 

$\gamma = \dfrac{\delta_s}{L}$

 

The ratio of the shear stress τ and the shear strain γ is called the modulus of elasticity in shear or modulus of rigidity and is denoted as G, in MPa.
 

$G = \dfrac{\tau}{\gamma}$

 

The relationship between the shearing deformation and the applied shearing force is
 

$\delta_s = \dfrac{VL}{A_s G} = \dfrac{\tau L}{G}$

 

where V is the shearing force acting over an area As.
 

Solution to Problem 211 Axial Deformation

Problem 211
A bronze bar is fastened between a steel bar and an aluminum bar as shown in Fig. p-211. Axial loads are applied at the positions indicated. Find the largest value of P that will not exceed an overall deformation of 3.0 mm, or the following stresses: 140 MPa in the steel, 120 MPa in the bronze, and 80 MPa in the aluminum. Assume that the assembly is suitably braced to prevent buckling. Use Est = 200 GPa, Eal = 70 GPa, and Ebr = 83 GPa.
 

Figure P-211