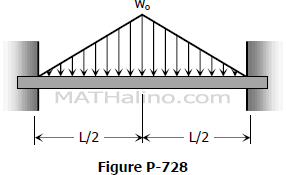
Problem 728 | Isosceles triangular load over the entire span of fully restrained beam
Problem 728
Determine the end moment and maximum deflection of a perfectly restrained beam loaded as shown in Fig. P-728.
Problem 721 | Propped beam with decreasing load by moment-area method
Problem 721
By the use of moment-are method, determine the magnitude of the reaction force at the left support of the propped beam in Fig. P-706.
Problem 720 | Propped beam with increasing load by moment-area method
Problem 720
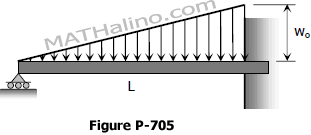
Find the reaction at the simple support of the propped beam shown in Fig. P-705 by using moment-area method.
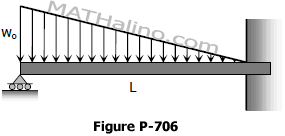
Problem 706 | Solution of Propped Beam with Decreasing Load
Example 03
The propped beam shown in Fig. P -706 is loaded by decreasing triangular load varying from wo from the simple end to zero at the fixed end. Find the support reactions and sketch the shear and moment diagrams
Problem 705 | Solution of Propped Beam with Increasing Load
Problem 705
Find the reaction at the simple support of the propped beam shown in Fig. P-705 and sketch the shear and moment diagrams.
Problem 657 | Beam Deflection by Conjugate Beam Method
Problem 657
Determine the midspan value of EIδ for the beam shown in Fig. P-657.
- Read more about Problem 657 | Beam Deflection by Conjugate Beam Method
- Log in or register to post comments
Problem 334 | Equilibrium of Parallel Force System
Problem 334
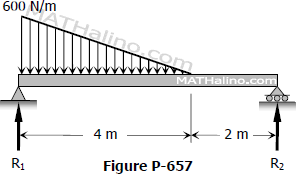
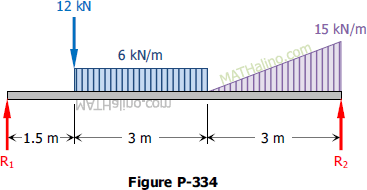
Determine the reactions for the beam loaded as shown in Fig. P-334.
- Read more about Problem 334 | Equilibrium of Parallel Force System
- Log in or register to post comments
Problem 333 | Equilibrium of Parallel Force System
Problem 333
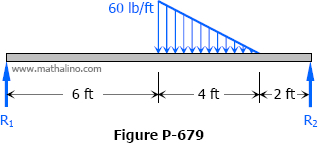
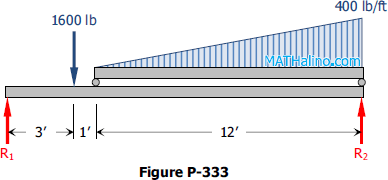
Determine the reactions R1 and R2 of the beam in Fig. P-333 loaded with a concentrated load of 1600 lb and a load varying from zero to an intensity of 400 lb per ft.
- Read more about Problem 333 | Equilibrium of Parallel Force System
- Log in or register to post comments
Solution to Problem 679 | Midspan Deflection
Problem 679
Determine the midspan value of EIδ for the beam shown in Fig. P-679 that carries a uniformly varying load over part of the span.
- Read more about Solution to Problem 679 | Midspan Deflection
- Log in or register to post comments