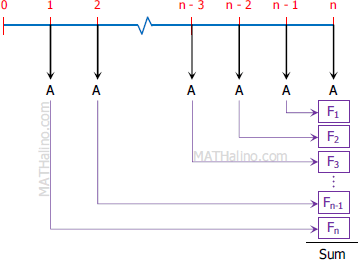
Investment of P250,000.00 per year

Situation
An investment of P250,000 is made at the end of each year with interest of 2.5% compounded annually.

  1. Determine the equal-payment-series compound-amount factor after 10 years.
    A.   11.203 C.   9.632
    B.   10.578 D.   8.736
  2. Determine the total amount of the investment after 10 years.
    A.   P2,800,000.00 C.   P2,400,000.00
    B.   P2,600,000.00 D.   P2,200,000.00
  3. How long (in years) will it take for the investment to amount to P10,000,000.00?
    A.   25 C.   15
    B.   18 D.   28

 

Derivation of Formula for the Future Amount of Ordinary Annuity

The sum of ordinary annuity is given by
 

$F = \dfrac{A[ \, (1 + i)^n - 1 \, ]}{i}$

 

To learn more about annuity, see this page: ordinary annuity, deferred annuity, annuity due, and perpetuity.
 

Derivation

Figure for Derivation of Sum of Ordinary Annuity

 

$F = \text{ Sum}$

$F = A + F_1 + F_2 + F_3 + \cdots + F_{n-1} + F_n$

$F = A + A(1 + i) + A(1 + i)^2 + A(1 + i)^3 + \cdots + A(1 + i)^{n-1} + A(1 + i)^n$