moment over the support
Problem 824 | Continuous Beam by Three-Moment Equation
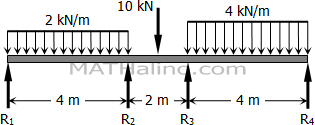
Problem 824
The first span of a simply supported continuous beam is 4 m long, the second span is 2 m long and the third span is 4 m long. Over the first span there is a uniformly distributed load 2 kN/m, and over the third span there is a uniformly distributed load of 4 kN/m. At the midpoint of the second span, there is a concentrated load of 10 kN. Solve for the moment over the supports and check your answers using Problems 820 and 821.
- Read more about Problem 824 | Continuous Beam by Three-Moment Equation
- Log in or register to post comments
Problem 823 | Continuous Beam by Three-Moment Equation
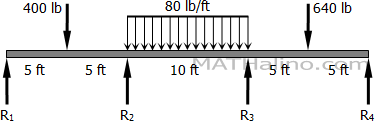
Problem 823
A continuous beam simply supported over three 10-ft spans carries a concentrated load of 400 lb at the center of the first span, a concentrated load of 640 lb at the center of the third span and a uniformly distributed load of 80 lb/ft over the middle span. Solve for the moment over the supports and check your answers using the results obtained for Problems 819 and 822.
- Read more about Problem 823 | Continuous Beam by Three-Moment Equation
- Log in or register to post comments
Problem 822 | Continuous Beam by Three-Moment Equation
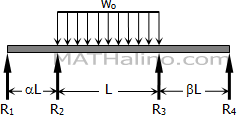
Problem 822
Solve Prob. 821 if the concentrated load is replaced by a uniformly distributed load of intensity wo over the middle span.
Answers:
$M_2 = -\dfrac{w_o L^2}{4} \cdot \dfrac{1 + 2\beta}{4(\alpha + 1)(1 + \beta) - 1}$
$M_3 = -\dfrac{w_o L^2}{4} \cdot \dfrac{1 + 2\alpha}{4(1 + \alpha)(1 + \beta) - 1}$
- Read more about Problem 822 | Continuous Beam by Three-Moment Equation
- Log in or register to post comments
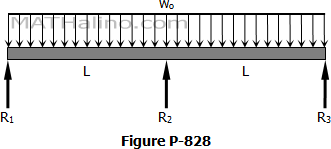
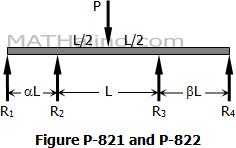
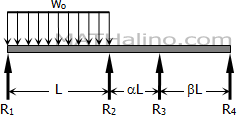
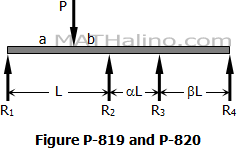
Problem 820 | Continuous Beam by Three-Moment Equation
Problem 820
Solve Prob. 819 if the concentrated load is replaced by a uniformly distributed load of intensity wo over the first span.
- Read more about Problem 820 | Continuous Beam by Three-Moment Equation
- Log in or register to post comments