equilibrium

Problem 351
The beam shown in Fig. P-351 is supported by a hinge at A and a roller on a 1 to 2 slope at B. Determine the resultant reactions at A and B.
 

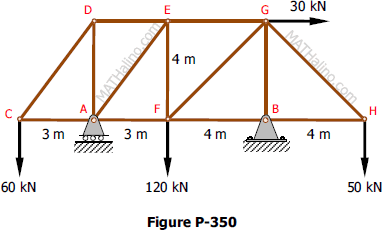
Problem 350
Compute the total reactions at A and B for the truss shown in Fig. P-350.
 

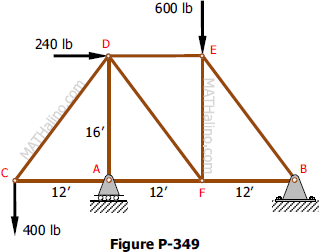
Problem 349
The truss shown in Fig. P-349 is supported on roller at A and hinge at B. Solve for the components of the reactions.
 

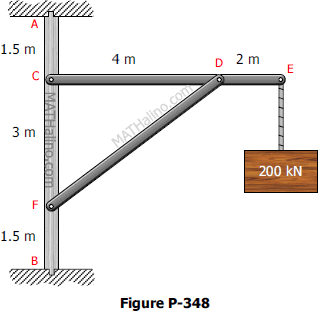
Problem 348
The frame shown in Fig. P-348 is supported in pivots at A and B. Each member weighs 5 kN/m. Compute the horizontal reaction at A and the horizontal and vertical components of the reaction at B.
 

Problem 347
Repeat Problem 346 if the cable pulls the boom AB into a position at which it is inclined at 30° above the horizontal. The loads remain vertical.
 

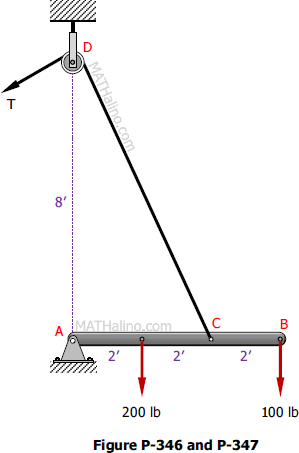
Problem 346
A boom AB is supported in a horizontal position by a hinge A and a cable which runs from C over a small pulley at D as shown in Fig. P-346. Compute the tension T in the cable and the horizontal and vertical components of the reaction at A. Neglect the size of the pulley at D.
 

There are three equilibrium conditions that can be used for non-concurrent, non-parallel force system.
 

The sum of all forces in the x-direction or horizontal is zero.

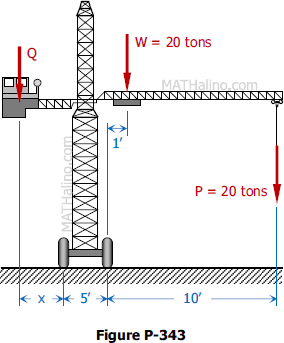
Problem 343
The weight W of a traveling crane is 20 tons acting as shown in Fig. P-343. To prevent the crane from tipping to the right when carrying a load P of 20 tons, a counterweight Q is used. Determine the value and position of Q so that the crane will remain in equilibrium both when the maximum load P is applied and when the load P is removed.
 

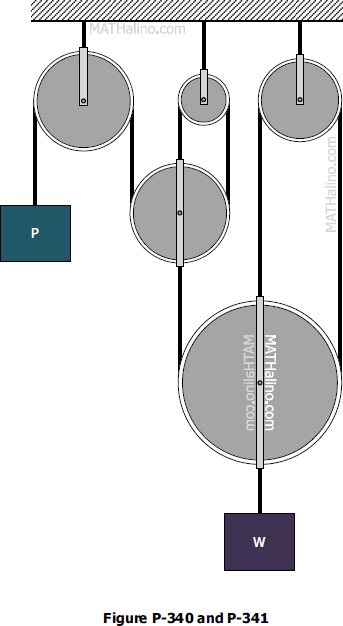
Problem 340
For the system of pulleys shown in Fig. P-340, determine the ratio of W to P to maintain equilibrium. Neglect axle friction and the weights of the pulleys.