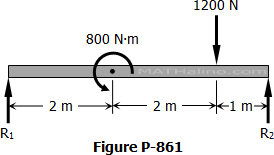
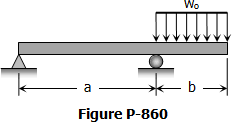
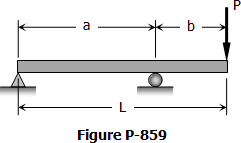
MATHalinoEngineering Math Review
MATHalinoEngineering Math ReviewBreadcrumbs
Home • Forums • Blogs • Glossary • Recent
About • Contact us • Terms of Use • Privacy Policy • Hosted by Linode • Powered by Drupal
About • Contact us • Terms of Use • Privacy Policy • Hosted by Linode • Powered by Drupal
MATHalino - Engineering Mathematics • Copyright 2025 Jhun Vert • All rights reserved