Considering Head Loss

Problem 6
As shown in Figure 4-03, the smaller pipe is cut off a short distance past the reducer so that the jet springs free into the air. Compute the pressure at 1 if Q = 5 cfs of water. D₁ = 12 inches and D₂ = 4 inches. Assume that the jet has the diameter D₂, that the pressure in the jet is atmospheric and that the loss of head from point 1 to point 2 is 5 ft of water.
 

Problem 2
From Figure 4-01, the following head losses are known: From (1) to (2), 0 m; from (2) to (3), 0.60 m; from (3) to (4), 2.1 m; from (4) to (5), 0.3 m. Make a table showing elevation head, velocity head, pressure head, and total head at each of the five points. How high above the center of the pipe will water stands in the piezometer tubes (3) and (4)?
 

Problem 1
The water surface shown in Figure 4-01 is 6 m above the datum. The pipe is 150 mm in diameter and the total loss of head between point (1) in the water surface and point (5) in the jet is 3 m. Determine the velocity of flow in the pipe and the discharge Q.
 

Energy is defined as ability to do work. Both energy and work are measured in Newton-meter (or pounds-foot in English). Kinetic energy and potential energy are the two commonly recognized forms of energy. In a flowing fluid, potential energy may in turn be subdivided into energy due to position or elevation above a given datum, and energy due to pressure in the fluid. Head is the amount of energy per Newton (or per pound) of fluid.
 

Kinetic Energy and Velocity Head
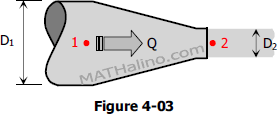
Kinetic energy is the ability of a mass to do work by virtue of its velocity. The kinetic energy of a mass M having a velocity v is ½Mv². Since M = W/g,

Elevation Energy and Elevation Head
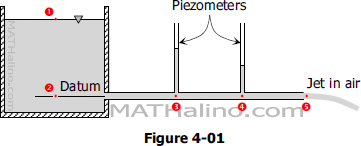
In connection to the action of gravity, elevation energy is manifested in a fluid by virtue of its position or elevation with respect to a horizontal datum plane.

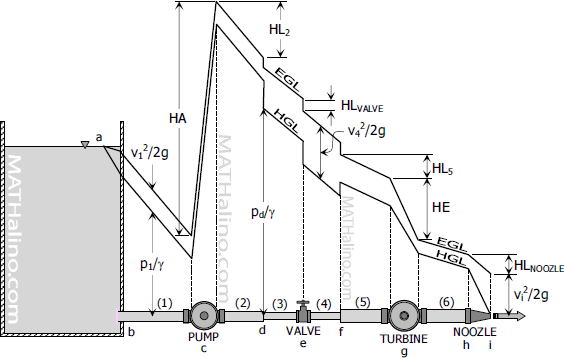
Pressure Energy and Pressure Head
A mass of fluid acquires pressure energy when it is in contact with other masses having some form of energy. Pressure energy therefore is an energy transmitted to the fluid by another mass that possesses some energy.