Beam Deflection

Problem 642
Find the maximum deflection for the cantilever beam loaded as shown in Figure P-642 if the cross section is 50 mm wide by 150 mm high. Use E = 69 GPa.
 

Problem 641
For the cantilever beam shown in Fig. P-641, what will cause zero deflection at A?
 

Problem 640
Compute the value of δ at the concentrated load in Prob. 639. Is the deflection upward downward?
 

Problem 639
The downward distributed load and an upward concentrated force act on the cantilever beam in Fig. P-639. Find the amount the free end deflects upward or downward if E = 1.5 × 10⁶ psi and I = 60 in⁴.
 

Problem 638
For the cantilever beam shown in Fig. P-638, determine the value of EIδ at the left end. Is this deflection upward or downward?
 

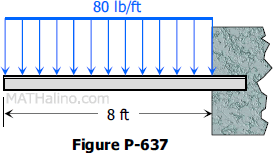
Problem 637
For the beam loaded as shown in Fig. P-637, determine the deflection 6 ft from the wall. Use E = 1.5 × 10⁶ psi and I = 40 in⁴.
 

Problem 636
The cantilever beam shown in Fig. P-636 has a rectangular cross-section 50 mm wide by h mm high. Find the height h if the maximum deflection is not to exceed 10 mm. Use E = 10 GPa.
 

Generally, the tangential deviation t is not equal to the beam deflection. In cantilever beams, however, the tangent drawn to the elastic curve at the wall is horizontal and coincidence therefore with the neutral axis of the beam. The tangential deviation in this case is equal to the deflection of the beam as shown below.