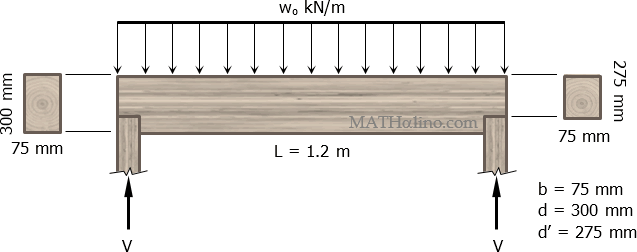
Example 01: Safe Uniform Load for a Beam that was Notched at the Tension Fibers at Supports
Problem
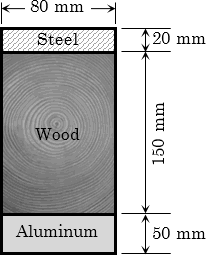
A 75 mm × 150 mm beam carries a uniform load wo over the entire span of 1.2 m. Square notches 25 mm deep are provided at the bottom of the beam at the supports. Calculate the safe value of wo based on shear alone.
Allowable shear normal to grain = 1.85 MPa