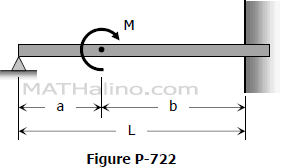
Problem 722 | Propped beam with moment load on the span by area-moment method
Problem 722
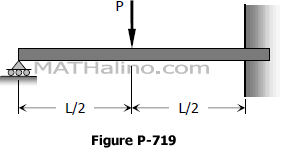
For the beam shown in Fig. P-722, compute the reaction R at the propped end and the moment at the wall. Check your results by letting b = L and comparing with the results in Problem 707.
Solution