Problem 654 | Beam Deflection by Conjugate Beam Method
Problem 654
For the beam in Fig. P-654, find the value of EIδ at 2 ft from R2.
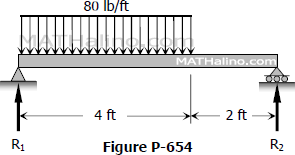
- Read more about Problem 654 | Beam Deflection by Conjugate Beam Method
- Log in or register to post comments
Problem 653 | Beam Deflection by Conjugate Beam Method
Problem 653
Compute the midspan value of EIδ for the beam shown in Fig. P-653. (Hint: Draw the M diagram by parts, starting from midspan toward the ends. Also take advantage of symmetry.
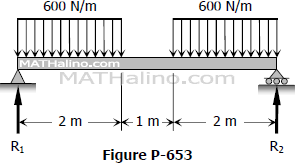
- Read more about Problem 653 | Beam Deflection by Conjugate Beam Method
- Log in or register to post comments
01 - Highest point of projectile as measured from inclined plane
Problem 01
A projectile is fired up the inclined plane at an initial velocity of 15 m/s. The plane is making an angle of 30° from the horizontal. If the projectile was fired at 30° from the incline, compute the maximum height z measured perpendicular to the incline that is reached by the projectile. Neglect air resistance.
Conjugate Beam Method | Beam Deflection
Deflection on real beam = Moment on conjugate beam
Properties of Conjugate Beam

Engr. Christian Otto Mohr
- The length of a conjugate beam is always equal to the length of the actual beam.
- The load on the conjugate beam is the M/EI diagram of the loads on the actual beam.
- Read more about Conjugate Beam Method | Beam Deflection
- Log in or register to post comments
Strain Energy Method (Castigliano’s Theorem) | Beam Deflection

Engr. Alberto Castigliano
Italian engineer Alberto Castigliano (1847 – 1884) developed a method of determining deflection of structures by strain energy method. His Theorem of the Derivatives of Internal Work of Deformation extended its application to the calculation of relative rotations and displacements between points in the structure and to the study of beams in flexure.
1012 Train at constant deceleration | Rectilinear Translation
Problem 1012
A train moving with constant acceleration travels 24 ft (7.32 m) during the 10th second of its motion and 18 ft (5.49 m) during the 12th second of its motion. Find its initial velocity and its constant acceleration.
02 Problem involving angle and median | Properties of a Triangle
Problem 02
From the figure shown below, angle CAD = angle BCD = theta and CD is a median of triangle ABC through vertex C. Determine the value of the angle theta.

Solving for angle $A$ in triangle ABC
Problem 10
In a triangle ABC, if $\dfrac{2 \cos A}{a} + \dfrac{\cos B}{b} + \dfrac{2 \cos C}{c} = \dfrac{a}{bc} + \dfrac{b}{ca}$, find the value of angle $A$.
- Read more about Solving for angle $A$ in triangle ABC
- Log in or register to post comments
Problem 10 | Special Products and Factoring
Problem 10
Given that $x + y + xy = 1$, where $x$ and $y$ are nonzero real numbers,find the value of $xy + \dfrac{1}{xy} - \dfrac{y}{x} - \dfrac{x}{y}$.
- Read more about Problem 10 | Special Products and Factoring
- Log in or register to post comments
1011 Time of launching a ship | Rectilinear Translation
Problem 1011
A ship being launched slides down the ways with constant acceleration. She takes 8 sec to slide (the first foot | 0.3048 meter). How long will she take to slide down the ways if their length is (625 ft | 190.5 m)?
