August 2010

Problem 30
Two railroad tracks intersect at right angles, at noon there is a train on each track approaching the crossing at 40 mi/hr, one being 100 mi, the other 200 mi distant. Find (a) when they will be nearest together, and (b) what will be their minimum distance apart.
 

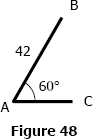Problem 28
At noon a car drives from A (Fig. 48) toward C at 60 miles per hour. Another car starting from B at the same time drives toward A at 30 miles per hour. If AB = 42 miles, find when the cars will be nearest each other.
 
 

Problem 26
A kite is 40 ft high with 50 ft cord out. If the kite moves horizontally at 5 miles per hour directly away from the boy flying it, how fast is the cord being paid out?

Problem 22
One city C, is 30 miles north and 35 miles east from another city, D. At noon, a car starts north from C at 40 miles per hour, at 12:10 PM, another car starts east from D at 60 miles per hour. Find when the cars will be nearest together.

Problem 19
One city A, is 30 mi north and 55 mi east of another city, B. At noon, a car starts west from A at 40 mi/hr, at 12:10 PM, another car starts east from B at 60 mi/hr. Find, in two ways, when the cars will be nearest together.

Problem 17
A light is placed on the ground 30 ft from a building. A man 6 ft tall walks from the light toward the building at the rate of 5 ft/sec. Find the rate at which the length of his shadow is changing when he is 15 ft from the building.

Problem 15
A light at eye level stands 20 ft from a house and 15 ft from the path leading from the house to the street. A man walks along the path at 6 ft per sec. How fast does his shadow move along the wall when he is 5 ft from the house?

Problem 13
A trapezoidal trough is 10 ft long, 4 ft wide at the top, 2 ft wide at the bottom and 2 ft deep. If water flows in at 10 ft³/min, find how fast the surface is rising, when the water is 6 in deep.