Solution to Problem 670 | Deflections in Simply Supported Beams
Problem 670
Determine the value of EIδ at the left end of the overhanging beam shown in Fig. P-670.
May 2010
Solution to Problem 669 | Deflections in Simply Supported Beams
Problem 669
Compute the value of EIδ midway between the supports of the beam shown in Fig. P-669.
Solution to Problem 668 | Deflections in Simply Supported Beams
Problem 668
For the beam shown in Fig. P-668, compute the value of P that will cause the tangent to the elastic curve over support R2 to be horizontal. What will then be the value of EIδ under the 100-lb load?
Solution to Problem 667 | Deflections in Simply Supported Beams
Problem 667
Determine the value of EIδ at the right end of the overhanging beam shown in Fig. P-667. Is the deflection up or down?
Solution to Problem 666 | Deflections in Simply Supported Beams
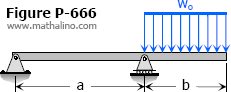
Problem 666
Determine the value of EIδ at the right end of the overhanging beam shown in Fig. P-666.
Solution to Problem 665 | Deflections in Simply Supported Beams
Problem 665
Replace the concentrated load in Prob. 664 by a uniformly distributed load of intensity wo acting over the middle half of the beam. Find the maximum deflection.
Solution to Problem 664 | Deflections in Simply Supported Beams
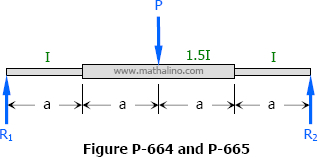
Problem 664
The middle half of the beam shown in Fig. P-664 has a moment of inertia 1.5 times that of the rest of the beam. Find the midspan deflection. (Hint: Convert the M diagram into an M/EI diagram.)
Solution to Problem 663 | Deflections in Simply Supported Beams
Problem 663
Determine the maximum deflection of the beam carrying a uniformly distributed load over the middle portion, as shown in Fig. P-663. Check your answer by letting 2b = L.
Solution to Problem 662 | Deflections in Simply Supported Beams
Problem 662
Determine the maximum deflection of the beam shown in Fig. P-662. Check your result by letting a = L/2 and comparing with case 8 in Table 6-2. Also, use your result to check the answer to Prob. 653.
Solution to Problem 661 | Deflections in Simply Supported Beams
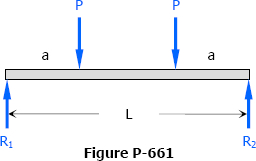
Problem 661
Compute the midspan deflection of the symmetrically loaded beam shown in Fig. P-661. Check your answer by letting a = L/2 and comparing with the answer to Problem 609.
