Uniformly Distributed Load

Problem 666
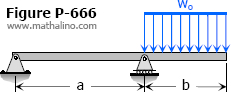
Determine the value of EIδ at the right end of the overhanging beam shown in Fig. P-666.
 

Problem 665
Replace the concentrated load in Prob. 664 by a uniformly distributed load of intensity w_o acting over the middle half of the beam. Find the maximum deflection.
 

Problem 663
Determine the maximum deflection of the beam carrying a uniformly distributed load over the middle portion, as shown in Fig. P-663. Check your answer by letting 2b = L.
 

Problem 654
For the beam in Fig. P-654, find the value of EIδ at 2 ft from R₂. (Hint: Draw the reference tangent to the elastic curve at R₂.)
 

Problem 653
Compute the midspan value of EIδ for the beam shown in Fig. P-653. (Hint: Draw the M diagram by parts, starting from midspan toward the ends. Also take advantage of symmetry to note that the tangent drawn to the elastic curve at midspan is horizontal.)
 

Coplanar Parallel Force System
Parallel forces can be in the same or in opposite directions. The sign of the direction can be chosen arbitrarily, meaning, taking one direction as positive makes the opposite direction negative. The complete definition of the resultant is according to its magnitude, direction, and line of action.
 

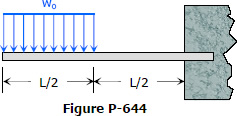
Problem 644
Determine the maximum deflection for the beam loaded as shown in Fig. P-644.
 

Problem 640
Compute the value of δ at the concentrated load in Prob. 639. Is the deflection upward downward?
 

Problem 639
The downward distributed load and an upward concentrated force act on the cantilever beam in Fig. P-639. Find the amount the free end deflects upward or downward if E = 1.5 × 10⁶ psi and I = 60 in⁴.
 

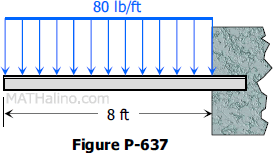
Problem 637
For the beam loaded as shown in Fig. P-637, determine the deflection 6 ft from the wall. Use E = 1.5 × 10⁶ psi and I = 40 in⁴.