rigid block

Problem 350
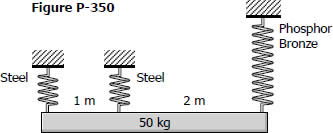
As shown in Fig. P-350, a homogeneous 50-kg rigid block is suspended by the three springs whose lower ends were originally at the same level. Each steel spring has 24 turns of 10-mm-diameter on a mean diameter of 100 mm, and G = 83 GPa. The bronze spring has 48 turns of 20-mm-diameter wire on a mean diameter of 150 mm, and G = 42 GPa. Compute the maximum shearing stress in each spring using Eq. (3-9).
 

Problem 239
The rigid platform in Fig. P-239 has negligible mass and rests on two steel bars, each 250.00 mm long. The center bar is aluminum and 249.90 mm long. Compute the stress in the aluminum bar after the center load P = 400 kN has been applied. For each steel bar, the area is 1200 mm2 and E = 200 GPa. For the aluminum bar, the area is 2400 mm2 and E = 70 GPa.
 

Problem 238
The lower ends of the three bars in Fig. P-238 are at the same level before the uniform rigid block weighing 40 kips is attached. Each steel bar has a length of 3 ft, and area of 1.0 in.², and E = 29 × 10⁶ psi. For the bronze bar, the area is 1.5 in.² and E = 12 × 10⁶ psi. Determine (a) the length of the bronze bar so that the load on each steel bar is twice the load on the bronze bar, and (b) the length of the bronze that will make the steel stress twice the bronze stress.