Pressure Head

Problem 5
With 30 L/s of water flowing in Figure 4-02, what pressure must be maintained at 1 if the pressure at 2 is to be 70 kPa and the loss of head between 1 and 2 is 5 percent of the difference in pressure head at 1 and 2.
 

Problem 4
In Figure 4-02, with 15 L/s of water flowing from 1 to 2 the pressure at 1 is 100 kPa and at 2 is 70 kPa. Compute the loss of head between 1 and 2.
 

Problem 3
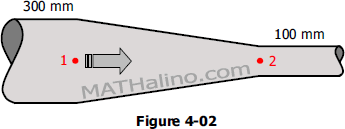
A 300-mm pipe is connected by a reducer to a 100-mm pipe. See Figure 4-02. Points 1 and 2 are at the same elevation, the pressure at 1 is 200 kPa. The discharge Q is 30 liters per second flowing from 1 to 2 and the energy lost from 1 to 2 is equivalent to 20 kPa.

1. Compute the pressure at 2 if the liquid is water.
2. Compute the pressure at 2 if the liquid is oil (sp gr = 0.80).
3. Compute the pressure at 2 if the liquid is molasses (sp gr = 1.5).

Problem 2
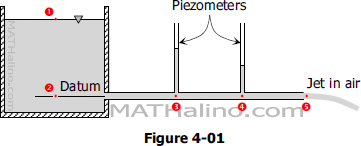
From Figure 4-01, the following head losses are known: From (1) to (2), 0 m; from (2) to (3), 0.60 m; from (3) to (4), 2.1 m; from (4) to (5), 0.3 m. Make a table showing elevation head, velocity head, pressure head, and total head at each of the five points. How high above the center of the pipe will water stands in the piezometer tubes (3) and (4)?
 

Energy is defined as ability to do work. Both energy and work are measured in Newton-meter (or pounds-foot in English). Kinetic energy and potential energy are the two commonly recognized forms of energy. In a flowing fluid, potential energy may in turn be subdivided into energy due to position or elevation above a given datum, and energy due to pressure in the fluid. Head is the amount of energy per Newton (or per pound) of fluid.
 

Kinetic Energy and Velocity Head
Kinetic energy is the ability of a mass to do work by virtue of its velocity. The kinetic energy of a mass M having a velocity v is ½Mv². Since M = W/g,

Elevation Energy and Elevation Head
In connection to the action of gravity, elevation energy is manifested in a fluid by virtue of its position or elevation with respect to a horizontal datum plane.

Pressure Energy and Pressure Head
A mass of fluid acquires pressure energy when it is in contact with other masses having some form of energy. Pressure energy therefore is an energy transmitted to the fluid by another mass that possesses some energy.

Manometer is a simple and inexpensive device of measuring pressure and pressure difference. It is usually bent to form a U-tube and filled with liquid of known specific gravity. The surface of the liquid will move in proportion to changes of pressure.
 

Problem
A pressure gage on the discharge side of a pump reads 300 kPa. Oil (sp gr 0.82) is being pumped. Compute the pressure head in meters of oil.
 

Problem
The pressure in a gas tank is 2.75 atmospheres. Compute the pressure in kiloPascal and the pressure head in meter of water.
 

Consider two points 1 and 2 lie in the ends of fluid prism having a cross-sectional area dA and length L. The difference in elevation between these two points is h as shown in Figure 02 below. The fluid is at rest and its surface is free. The prism is therefore in equilibrium and all forces acting on it sums up to zero.
 

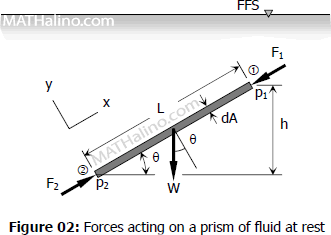
Note: FFS stands for Free Fluid Surface which refers to fluid surface subject to zero gauge pressure.