parallel forces

Problem 334
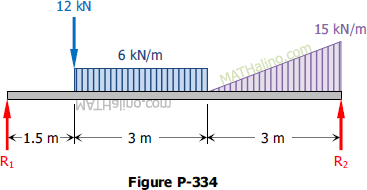
Determine the reactions for the beam loaded as shown in Fig. P-334.
 

Problem 333
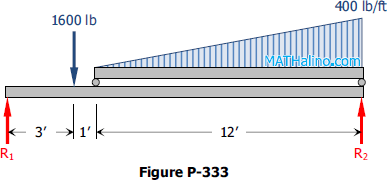
Determine the reactions R₁ and R₂ of the beam in Fig. P-333 loaded with a concentrated load of 1600 lb and a load varying from zero to an intensity of 400 lb per ft.
 

Problem 332
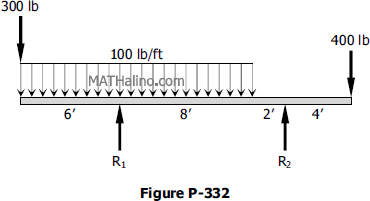
Determine the reactions for the beam shown in Fig. P-332.
 

Couple is a system of forces whose magnitude of the resultant is zero and yet has a moment sum. Geometrically, couple is composed of two equal forces that are parallel to each other and acting in opposite direction. The magnitude of the couple is given by
 

 
Where $F$ are the two forces and $d$ is the moment arm, or the perpendicular distance between the forces.
 

Problem 242
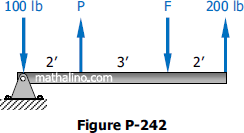
Find the value of P and F so that the four forces shown in Fig. P-242 produce an upward resultant of 300 lb acting at 4 ft from the left end of the bar.
 

Problem 241
Locate the amount and position of the resultant of the loads acting on the Fink truss in Fig. P-241.
 

Problem 240
The shaded area in Fig P-240 represents a steel plate of uniform thickness. A hole of 4-in. diameter has been cut in the plate. Locate the center of gravity the plate. Hint: The weight of the plate is equivalent to the weight of the original plate minus the weight of material cut away. Represent the original plate weight of plate by a downward force acting at the center of the 10 × 14 in. rectangle. Represent the weight of the material cut away by an upward force acting at the center of the circle. Locate the position of the resultant of these two forces with respect to the left edge and bottom of the plate.
 

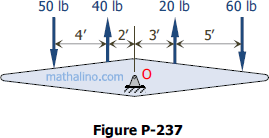
Problem 237
Determine the resultant of the four parallel forces acting on the rocker arm of Fig. P-237.
 

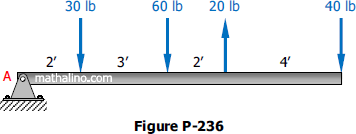
Problem 236
A parallel force system acts on the lever shown in Fig. P-236. Determine the magnitude and position of the resultant.
 

Coplanar Parallel Force System
Parallel forces can be in the same or in opposite directions. The sign of the direction can be chosen arbitrarily, meaning, taking one direction as positive makes the opposite direction negative. The complete definition of the resultant is according to its magnitude, direction, and line of action.