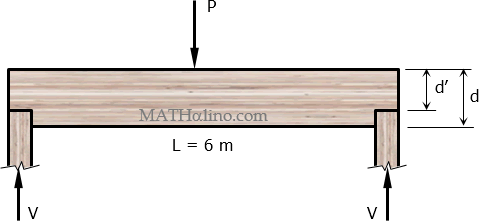
Example 02: Notched beam with concentrated load

Problem
A 150 mm by 300 mm wooden beam having a simple span of 6 meters carries a concentrated load P at its midspan. It is notched at the supports as shown in the figure. For this problem, all calculations are based on shear alone using the 2010 NSCP specification given below. Allowable shear stress of wood, Fv = 1.0 MPa.
 

notched-beam-002-concentrated-load.gif

 

  1. If P = 30 kN, calculate the maximum allowable depth (millimeters) of notches at the supports.
    1. 88
    2. 62
    3. 238
    4. 212
  2. If the depth of notches is 100 mm, what is the safe value of P (kiloNewton) the beam can carry.
    1. 26.67
    2. 17.78
    3. 8.89
    4. 13.33
  3. If P = 25 kN and the depth of notches is 150 millimeters, what is the shear stress (MegaPascal) near the supports.
    1. 0.83
    2. 6.67
    3. 1.67
    4. 3.33

 

NSCP 2010 Section 616.4: Horizontal Shear in Notched Beams
When rectangular-shaped girder, beams or joists are notched at points of support on the tension side, they shall meet the design requirements of that section in bending and in shear. The horizontal shear stress at such point shall be calculated by:
 

$f_v = \dfrac{3V}{2bd'}\left( \dfrac{d}{d'} \right)^2$

Where:

$d$ = total depth of beam.
$d'$ = actual depth of beam at notch.

 

Example 01: Safe Uniform Load for a Beam that was Notched at the Tension Fibers at Supports

Problem
A 75 mm × 150 mm beam carries a uniform load wo over the entire span of 1.2 m. Square notches 25 mm deep are provided at the bottom of the beam at the supports. Calculate the safe value of wo based on shear alone.

Allowable shear parallel to grain = 1.40 MPa
Allowable shear normal to grain = 1.85 MPa
notched-beam-001-uniform-load.gif

 

Notching on Beams

NSCP 2001
When rectangular shaped girders, beams or joists are notched at points of supports on the tension side, the horizontal shear stress at such point shall not exceed:
 

$F_v = \dfrac{3V}{2bd'}\left( \dfrac{d}{d'} \right)$

Where

$d$ = total depth of beam
$d'$ = actual depth of beam at notch