01 Rectangle of maximum perimeter inscribed in a circle
Problem 01
Find the shape of the rectangle of maximum perimeter inscribed in a circle.
Maxima and Minima
Maxima and Minima Using Trigonometric Functions
Many problems in application of maxima and minima may be solved easily by making use of trigonometric functions. The basic idea is the same; identify the constant terms and identify the variable to be maximized or minimized, differentiate that variable then equate to zero.
- Read more about Maxima and Minima Using Trigonometric Functions
- Log in or register to post comments
28-29 Time Rates: Two cars driving on roads that intersects at 60 degree
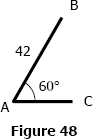Problem 28
At noon a car drives from A (Fig. 48) toward C at 60 miles per hour. Another car starting from B at the same time drives toward A at 30 miles per hour. If AB = 42 miles, find when the cars will be nearest each other.
22-24 One car from a city starts north, another car from nearby city starts east
Problem 22
One city C, is 30 miles north and 35 miles east from another city, D. At noon, a car starts north from C at 40 miles per hour, at 12:10 PM, another car starts east from D at 60 miles per hour. Find when the cars will be nearest together.
72 - 74 Light intensity of illumination and theory of attraction
Problem 72
A light is to be placed above the center of a circular area of radius a. What height gives the best illumination on a circular walk surrounding the area? (When light from a point source strikes a surface obliquely, the intensity of illumination is
$I = \dfrac{k \sin \theta}{d^2}$
where θ is the angle of incidence and d the distance from the source.)
69 - 71 Shortest and most economical path of motorboat
Problem 69
A man on an island 12 miles south of a straight beach wishes to reach a point on shore 20 miles east. If a motorboat, making 20 miles per hour, can be hired at the rate of \$2.00 per hour for the time it is actually used, and the cost of land transportation is \$0.06 per mile, how much must he pay for the trip?
- Read more about 69 - 71 Shortest and most economical path of motorboat
- Log in or register to post comments
66 - 68 Maxima and minima: Pyramid inscribed in a sphere and Indian tepee
Problem 66
Find the largest right pyramid with a square base that can be inscribed in a sphere of radius a.
64 - 65 Maxima and minima: cone inscribed in a sphere and cone circumscribed about a sphere
Problem 64
A sphere is cut to the shape of a circular cone. How much of the material can be saved? (See Problem 63).
62 - 63 Maxima and minima: cylinder inscribed in a cone and cone inscribed in a sphere
Problem 62
Inscribe a circular cylinder of maximum convex surface area in a given circular cone.
60 - 61 Maxima and minima problems of a folded page
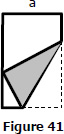Problem 60
One corner of a leaf of width a is folded over so as just to reach the opposite side of the page. Find the width of the part folded over when the length of the crease is a minimum. See Figure 41.
- Read more about 60 - 61 Maxima and minima problems of a folded page
- Log in or register to post comments