Discharge

Problem 6
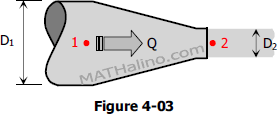
As shown in Figure 4-03, the smaller pipe is cut off a short distance past the reducer so that the jet springs free into the air. Compute the pressure at 1 if Q = 5 cfs of water. D₁ = 12 inches and D₂ = 4 inches. Assume that the jet has the diameter D₂, that the pressure in the jet is atmospheric and that the loss of head from point 1 to point 2 is 5 ft of water.
 

Problem 1
The water surface shown in Figure 4-01 is 6 m above the datum. The pipe is 150 mm in diameter and the total loss of head between point (1) in the water surface and point (5) in the jet is 3 m. Determine the velocity of flow in the pipe and the discharge Q.
 

Problem 1
Compute the discharge of water through 75 mm pipe if the mean velocity is 2.5 m/sec.
 

Problem 2
The discharge of air through a 600-mm pipe is 4 m³/sec. Compute the mean velocity in m/sec.
 

Problem 3
A pipe line consists of successive lengths of 380-mm, 300-mm, and 250-mm pipe. With a continuous flow through the line of 250 Lit/sec of water, compute the mean velocity in each size of pipe.
 

Discharge (also called flow rate)
The amount of fluid passing a section of a stream in unit time is called the discharge. If v is the mean velocity and A is the cross sectional area, the discharge Q is defined by Q = Av which is known as volume flow rate. Discharge is also expressed as mass flow rate and weight flow rate.