Login here. Registration is temporarily disabled.
MATHalinoEngineering Math ReviewSituation
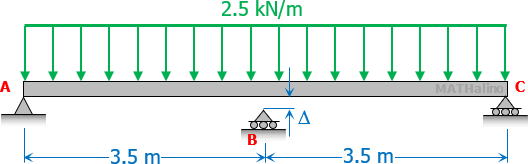
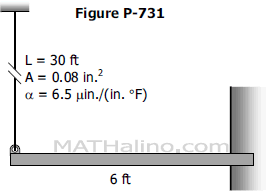
A beam of uniform cross section whose flexural rigidity EI = 2.8 × 1011 N·mm2, is placed on three supports as shown. Support B is at small gap Δ so that the moment at B is zero.
1. Calculate the reaction at A.
| A. 4.375 kN | C. 5.437 kN |
| B. 8.750 kN | D. 6.626 kN |
2. What is the reaction at B?
| A. 4.375 kN | C. 5.437 kN |
| B. 8.750 kN | D. 6.626 kN |
3. Find the value of Δ.
| A. 46 mm | C. 34 mm |
| B. 64 mm | D. 56 mm |
Problem 868
Determine the values of EIδ at midspan and at the ends of the beam loaded as shown in Figure P-868.
Problem 861
For the beam shown in Fig. P-861, determine the value of EIδ at 2 m and 4 m from the left support.
Problem 732
The midpoint of the steel in Fig. P-732 is connected to the vertical aluminum rod. Determine the maximum value of P if the stress in the rod is not to exceed 120 MPa.
Problem 731
The beam shown in Fig. P-731 is connected to a vertical rod. If the beam is horizontal at a certain temperature, determine the increase in stress in the rod if the temperature of the rod drops 90°F. Both the beam and the rod are made of steel with E = 29 × 106 psi. For the beam, use I = 154 in.4
Problem 705
Find the reaction at the simple support of the propped beam shown in Fig. P-705 and sketch the shear and moment diagrams.
Problem 704
Find the reactions at the supports and draw the shear and moment diagrams of the propped beam shown in Fig. P-704.
There are 12 cases listed in the method of superposition for beam deflection.
See beam deflection by superposition method for details.
Problem 658
For the beam shown in Fig. P-658, find the value of EIδ at the point of application of the couple.
Problem 657
Determine the midspan value of EIδ for the beam shown in Fig. P-657.
