beam reaction

Problem 833
Refer to Problem 825 for which M₂ = -980 lb·ft and M₃ = -1082 lb·ft.
 

Problem 829
A uniform load is carried over three equal spans as shown in Fig. P-829.
 

Problem 352
A pulley 4 ft in diameter and supporting a load 200 lb is mounted at B on a horizontal beam as shown in Fig. P-352. The beam is supported by a hinge at A and rollers at C. Neglecting the weight of the beam, determine the reactions at A and C.
 

Problem 351
The beam shown in Fig. P-351 is supported by a hinge at A and a roller on a 1 to 2 slope at B. Determine the resultant reactions at A and B.
 

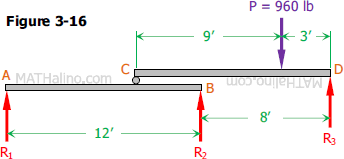
Problem 338
The two 12-ft beams shown in Fig. 3-16 are to be moved horizontally with respect to each other and load P shifted to a new position on CD so that all three reactions are equal. How far apart will R₂ and R₃ then be? How far will P be from D?
 

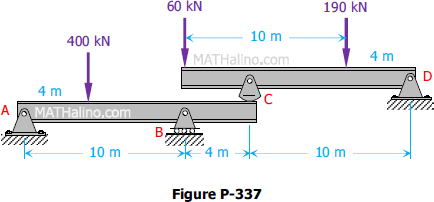
Problem 337
The upper beam in Fig. P-337 is supported at D and a roller at C which separates the upper and lower beams. Determine the values of the reactions at A, B, C, and D. Neglect the weight of the beams.
 

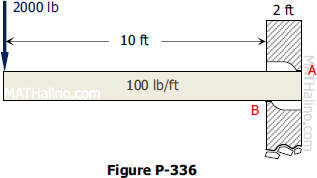
Problem 336
The cantilever beam shown in Fig. P-336 is built into a wall 2 ft thick so that it rests against points A and B. The beam is 12 ft long and weighs 100 lb per ft.
 

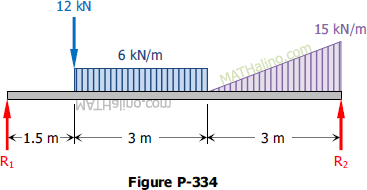
Problem 334
Determine the reactions for the beam loaded as shown in Fig. P-334.
 

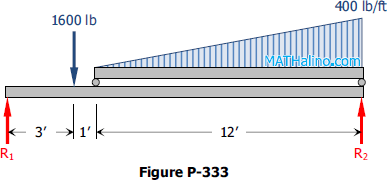
Problem 333
Determine the reactions R₁ and R₂ of the beam in Fig. P-333 loaded with a concentrated load of 1600 lb and a load varying from zero to an intensity of 400 lb per ft.
 

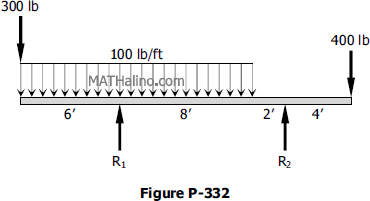
Problem 332
Determine the reactions for the beam shown in Fig. P-332.