Interest and Discount

Interest
The amount of money earned for the use of borrowed capital is called interest. From the borrower’s point of view, interest is the amount of money paid for the capital. For the lender, interest is the income generated by the capital which he has lent.
 

There are two types of interest, simple interest and compound interest.
 

Derivation of Formula for the Future Amount of Ordinary Annuity

The sum of ordinary annuity is given by
 

$F = \dfrac{A[ \, (1 + i)^n - 1 \, ]}{i}$

 

To learn more about annuity, see this page: ordinary annuity, deferred annuity, annuity due, and perpetuity.
 

Derivation

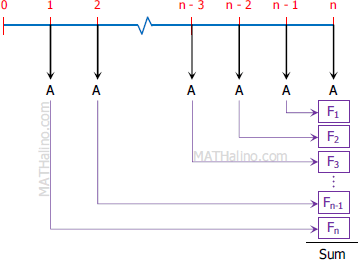
Figure for Derivation of Sum of Ordinary Annuity

 

$F = \text{ Sum}$

$F = A + F_1 + F_2 + F_3 + \cdots + F_{n-1} + F_n$

$F = A + A(1 + i) + A(1 + i)^2 + A(1 + i)^3 + \cdots + A(1 + i)^{n-1} + A(1 + i)^n$
 

Annuities and Capitalized Cost

Annuity
An annuity is a series of equal payments made at equal intervals of time. Financial activities like installment payments, monthly rentals, life-insurance premium, monthly retirement benefits, are familiar examples of annuity.
 

Annuity can be certain or uncertain. In annuity certain, the specific amount of payments are set to begin and end at a specific length of time. A good example of annuity certain is the monthly payments of a car loan where the amount and number of payments are known. In annuity uncertain, the annuitant may be paid according to certain event. Example of annuity uncertain is life and accident insurance. In this example, the start of payment is not known and the amount of payment is dependent to which event.
 

Problem 04 | Integrating Factors Found by Inspection

Problem 04
$2t \, ds + s(2 + s^2t) \, dt = 0$
 

Solution 04
$2t \, ds + s(2 + s^2t) \, dt = 0$

$2t \, ds + 2s \, dt + s^3t \, dt = 0$

$(2t \, ds + 2s \, dt) + s^3t \, dt = 0$

$2(t \, ds + s \, dt) + s^3t \, dt = 0$

$2 \, d(st) + s^3t \, dt = 0$

$\dfrac{2 \, d(st)}{s^3t^3} + \dfrac{s^3t \, dt}{s^3t^3} = 0$

$\dfrac{2 \, d(st)}{(st)^3} + \dfrac{dt}{t^2} = 0$

$2 (st)^{-3} \, d(st) + t^{-2} \, dt = 0$

$\displaystyle 2\int (st)^{-3} \, d(st) + \int t^{-2} \, dt = 0$

$-(st)^{-2} - t^{-1} = -c$

Problem 03 | Integrating Factors Found by Inspection

Problem 03
$(x^3y^3 + 1) \, dx + x^4y^2 \, dy = 0$
 

Solution 03
$(x^3y^3 + 1) \, dx + x^4y^2 \, dy = 0$

$x^3y^3 \, dx + dx + x^4y^2 \, dy = 0$

$(x^3y^3 \, dx + x^4y^2 \, dy) + dx = 0$

$x^3y^2(y \, dx + x \, dy) + dx = 0$

$x^3y^2 \, d(xy) + dx = 0$
 

Divide by x both sides
$x^2y^2 \, d(xy) + \dfrac{dx}{x} = 0$

$\displaystyle \int (xy)^2 \, d(xy) + \int \dfrac{dx}{x} = 0$

$\frac{1}{3}(xy)^3 + \ln x = -\ln c$

$x^3y^3 + 3\ln x = -3\ln c$

$x^3y^3 = -3\ln c - 3\ln x$

$x^3y^3 = -3(\ln c + \ln x)$

Problem 02 | Integrating Factors Found by Inspection

Problem 02
$y(y^3 - x) \, dx + x(y^3 + x) \, dy = 0$
 

Solution 02
$y(y^3 - x) \, dx + x(y^3 + x) \, dy = 0$

$y^4 \, dx - xy \, dx + xy^3 \, dy + x^2 \, dy = 0$

$(y^4 \, dx + xy^3 \, dy) - (xy \, dx - x^2 \, dy) = 0$

$y^3(y \, dx + x \, dy) - x(y \, dx - x \, dy) = 0$

$y^3 \, d(xy) - x(y \, dx - x \, dy) = 0$
 

Divide by y3
$d(xy) - \dfrac{x}{y} \left( \dfrac{y \, dx - x \, dy}{y^2} \right) = 0$

$d(xy) - \dfrac{x}{y} \, d\left( \dfrac{x}{y} \right) = 0$

Integrating Factors Found by Inspection

This section will use the following four exact differentials that occurs frequently.

  1. $d(xy) = x \, dy + y \, dx$
     
  2. $d\left( \dfrac{x}{y} \right) = \dfrac{y \, dx - x \, dy}{y^2}$
     
  3. $d\left( \dfrac{y}{x} \right) = \dfrac{x \, dy - y \, dx}{x^2}$
     
  4. $d\left( \arctan \dfrac{y}{x} \right) = \dfrac{x \, dy - y \, dx}{x^2 + y^2}$

    5.  

  5. $d\left( \arctan \dfrac{x}{y} \right) = \dfrac{y \, dx - x \, dy}{x^2 + y^2}$