Solution to Problem 117 Shear Stress
Problem 117
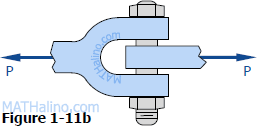
Find the smallest diameter bolt that can be used in the clevis shown in Fig. 1-11b if P = 400 kN. The shearing strength of the bolt is 300 MPa.
- Read more about Solution to Problem 117 Shear Stress
- Log in or register to post comments
Solution to Problem 116 Shear Stress
Problem 116
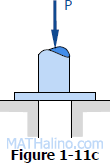
As in Fig. 1-11c, a hole is to be punched out of a plate having a shearing strength of 40 ksi. The compressive stress in the punch is limited to 50 ksi. (a) Compute the maximum thickness of plate in which a hole 2.5 inches in diameter can be punched. (b) If the plate is 0.25 inch thick, determine the diameter of the smallest hole that can be punched.
- Read more about Solution to Problem 116 Shear Stress
- Log in or register to post comments
Solution to Problem 115 Shear Stress
Problem 115
What force is required to punch a 20-mm-diameter hole in a plate that is 25 mm thick? The shear strength is 350 MN/m2.
- Read more about Solution to Problem 115 Shear Stress
- Log in or register to post comments
Shear Stress
Forces parallel to the area resisting the force cause shearing stress. It differs to tensile and compressive stresses, which are caused by forces perpendicular to the area on which they act. Shearing stress is also known as tangential stress.
where V is the resultant shearing force which passes through the centroid of the area A being sheared.
- Read more about Shear Stress
- Log in or register to post comments
Normal Stresses
Stress is defined as the strength of a material per unit area or unit strength. It is the force on a member divided by area, which carries the force, formerly express in psi, now in N/mm2 or MPa.
where P is the applied normal load in Newton and A is the area in mm2. The maximum stress in tension or compression occurs over a section normal to the load.
- Read more about Normal Stresses
- Log in or register to post comments
Strength of Materials
Reviewer in Strength of Materials
This page is the portal of the Reviewer in Strength of Materials. You can find here some basic theories and principles. Most of the content however for this online reviewer is solution to problems. You can find here a compiled step-by-step solution to problems in Strength of Materials. Feel free to explore the pages by selecting the topics tabulated below or browse it by chapters given as links below the tabulated data.
- Read more about Strength of Materials
- Log in or register to post comments
Solution to Problem 114 Normal Stress
Problem 114
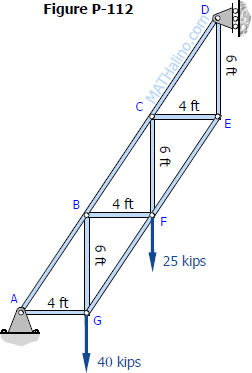
The homogeneous bar ABCD shown in Fig. P-114 is supported by a cable that runs from A to B around the smooth peg at E, a vertical cable at C, and a smooth inclined surface at D. Determine the mass of the heaviest bar that can be supported if the stress in each cable is limited to 100 MPa. The area of the cable AB is 250 mm2 and that of the cable at C is 300 mm2.
- Read more about Solution to Problem 114 Normal Stress
- Log in or register to post comments
Solution to Problem 113 Normal Stress
Problem 113
Find the stresses in members BC, BD, and CF for the truss shown in Fig. P-113. Indicate the tension or compression. The cross sectional area of each member is 1600 mm2.
- Read more about Solution to Problem 113 Normal Stress
- Log in or register to post comments
Solution to Problem 111 Normal Stress
Problem 111
For the truss shown in Fig. P-111, calculate the stresses in members CE, DE, and DF. The cross-sectional area of each member is 1.8 in2. Indicate tension (T) or compression (C).
- Read more about Solution to Problem 111 Normal Stress
- Log in or register to post comments