Solution to Problem 323 Torsion
Problem 323
A shaft composed of segments AC, CD, and DB is fastened to rigid supports and loaded as shown in Fig. P-323. For bronze, G = 35 GPa; aluminum, G = 28 GPa, and for steel, G = 83 GPa. Determine the maximum shearing stress developed in each segment.
- Read more about Solution to Problem 323 Torsion
- Log in or register to post comments
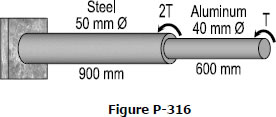
316 Permissible Torque That Can Be Applied to a Compound Shaft
Problem 316
A compound shaft consisting of a steel segment and an aluminum segment is acted upon by two torques as shown in Fig. P-316. Determine the maximum permissible value of T subject to the following conditions: τst ≤ 83 MPa, τal ≤ 55 MPa, and the angle of rotation of the free end is limited to 6°. For steel, G = 83 GPa and for aluminum, G = 28 GPa.
Solution to Problem 118 Shear Stress
Problem 118
A 200-mm-diameter pulley is prevented from rotating relative to 60-mm-diameter shaft by a 70-mm-long key, as shown in Fig. P-118. If a torque T = 2.2 kN·m is applied to the shaft, determine the width b if the allowable shearing stress in the key is 60 MPa.
- Read more about Solution to Problem 118 Shear Stress
- Log in or register to post comments